
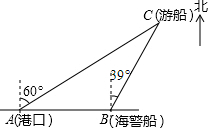
 如图,一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东39°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(结果精确到0.01小时)
如图,一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东39°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(结果精确到0.01小时) 分析 过点C作CD⊥AB交AB延长线于D.先解Rt△ACD得出CD=$\frac{1}{2}$AC=40海里,再解Rt△CBD中,得出BC=$\frac{CD}{cos∠BCD}$=$\frac{40}{cos39°}$海里,然后根据时间=路程÷速度即可求出海警船到大事故船C处所需的时间.
解答 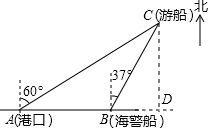 解:如图,过点C作CD⊥AB交AB延长线于D.
解:如图,过点C作CD⊥AB交AB延长线于D.
在Rt△ACD中,∵∠ADC=90°,∠CAD=30°,AC=80海里,
∴CD=$\frac{1}{2}$AC=40海里.
在Rt△CBD中,∵∠CDB=90°,∠BCD=37°,
∴BC=$\frac{CD}{cos∠BCD}$=$\frac{40}{cos39°}$海里,
∴海警船到大事故船C处所需的时间大约为:$\frac{40}{cos39°}$÷40=$\frac{1}{cos39°}$≈1.29(小时).
答:海警船到大事故船C处所需的大约时间为1.29小时.
点评 本题考查了解直角三角形的应用-方向角问题,难度适中,作出辅助线构造直角三角形是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | a>0,bc>0 | B. | a<0,bc<0 | C. | a<0,bc>0 | D. | a>0,bc<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
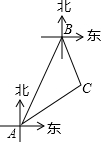 如图,点A、B是两个相距4000米的海岸观察点,点B位于点A的北偏东30°方向上,某日两观察点同时收到海面上的船C发出的信号,此时测得船C位于点A的北偏东60°方向上,位于点B的南偏东15°方向上,求此时船C到海岸AB的距离.(参考数据$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果精确到0.1米)
如图,点A、B是两个相距4000米的海岸观察点,点B位于点A的北偏东30°方向上,某日两观察点同时收到海面上的船C发出的信号,此时测得船C位于点A的北偏东60°方向上,位于点B的南偏东15°方向上,求此时船C到海岸AB的距离.(参考数据$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
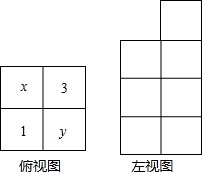 如图是由几何小立方体搭成的几何体的俯视图,正方形中的数字和字母表示叠在该位置上的小正方体的个数,再根据左视图,求x,y的值,并画出此时的主视图.
如图是由几何小立方体搭成的几何体的俯视图,正方形中的数字和字母表示叠在该位置上的小正方体的个数,再根据左视图,求x,y的值,并画出此时的主视图.查看答案和解析>>
科目:初中数学 来源:2017届山东省日照市莒县第三协作区九年级3月学业水平模拟考试数学试卷(解析版) 题型:单选题
如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )
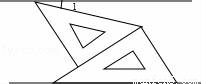
A. 30° B. 20° C. 15° D. 14°
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com