
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬��ABC=30�㣮��D��ֱ��BC�ϵ�һ�����㣬����AD������ADΪ����AD���Ҳ����ȱߡ�ADE��
��1����ͼ�٣�����Eǡ�����߶�BC��ʱ�����ж��߶�DE��BE��������ϵ�������ͼ��֤����Ľ��ۣ�
��2������E����ֱ��BC��ʱ������BE�������������䣬��1���н����Ƿ������������������ͼ�ڸ���֤����������������ֱ��д���µĽ��ۣ�
��3����AC=3����D��ֱ��BC���ƶ��Ĺ����У��Ƿ������A��C��D��EΪ������ı��������Σ�������ڣ�ֱ��д���߶�CD�ij��ȣ���������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺DE=BE���������£�
�ߡ�ADEΪ�ȱ������Σ�
��AD=DE=AE����AED=60�㣮
�ߡ�ABC=30�㣬��AED=��ABC+��EAB��
���EAB=60�㩁30��=30�㣬
���ABC=��EAB��
��EB=AE��
��EB=DE��
��2��
�⣺��ͼ��
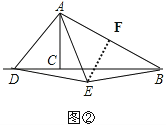
����E��EF��AB������ΪF��
�ڡ�ABC�У���ABC=30�㣬
���CAB=60�㣬
���DAE=��CAB��
���DAE����CAE=��BAC����CAE��
���CAD=��EAF��
�֡�AD=AE����ACD=��AFE��
���ADC�ա�AEF��
��AC=AF��
�ڡ�ABC�У���ABC=30�㣬
��AC= ![]() AB��
AB��
��AF=BF��
��EA=EB��
��DE=EB��
��3��
�⣺��ͼ��
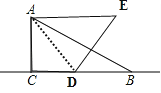
���ı���ACDE�����Σ���ACD=90�㣬
���CAE=90�㣮
�ߡ�CAE=��CAD+��EAD��
�֡�����������ADE�У���EAD=60�㣬
���CAD=30�㣮
��ֱ��������ACD�У�AC=3����CAD=30�㣬
�ɹ��ɶ����ɵ�CD= ![]() ��
��
ͬ���ɵã�����D���B�غϣ�ACƽ��DE����ʱCD=3 ![]() ��
��
������������AE��CD��CD= ![]() ������D���B�غϣ���ʱCD=3
������D���B�غϣ���ʱCD=3 ![]()
����������1�����õȱ������ε������Լ����������ε��ж���ɣ���2������E��EF��AB������ΪF��֤�á�ADC�ա�AEF�����ֱ����������30�ȵĽ����Ե�ֱ�DZ���б�ߵ�һ�������⣻��3����A��C��D��EΪ��������ε��������֣����ҳ��������ķ�����
�����㾫�����������⣬������Ҫ�˽�ȱ������ε�����(�ȱ������ε������Ƕ���Ȳ���ÿ���Ƕ���60��)����Ҫ���պ�30�Ƚǵ�ֱ��������(��ֱ���������У����һ����ǵ���30�㣬��ô�����Ե�ֱ�DZߵ���б�ߵ�һ��)�����֪ʶ���Ǵ���Ĺؼ���


 �¿α�����Ķ�ѵ��ϵ�д�
�¿α�����Ķ�ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��ƽ���ı���ABCD���ܳ���26cm���Խ���AC��BD�ཻ�ڵ�O�� AC��AB��E��BC���е㣬��AOD���ܳ�����AOB���ܳ���3cm����AE =_____cm��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ֽ������һ���ᣨ��ͼ�����۵�ֽ�森
��1������ʾ��1�ĵ����ʾ3�ĵ��غϣ��ش��������⣺
�ٱ�ʾ5�ĵ����ʾ��_________�ĵ��غϣ�
����������A��B����֮��ľ���Ϊ9��A��B����ࣩ����A��B���㾭�۵����غϣ���A��B�����ʾ�����Ƕ��٣�
��2������D��ʾ����Ϊx����xΪ_______ʱ��|x+1|��|x��2|��ֵ��ȣ�
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijũ���а���������Ķ������Ͷ��![]() Ԫ���ջ�ˮ���ܲ���Ϊ
Ԫ���ջ�ˮ���ܲ���Ϊ![]() ǧ�ˣ���ˮ�����г���ÿǧ����
ǧ�ˣ���ˮ�����г���ÿǧ����![]() Ԫ���ڹ�ֱ������ÿǧ����
Ԫ���ڹ�ֱ������ÿǧ����![]() Ԫ
Ԫ![]() ����ũ����ˮ�������г�����ƽ��ÿ�����
����ũ����ˮ�������г�����ƽ��ÿ�����![]() ǧ�ˣ���
ǧ�ˣ���![]() �˰�æ��ÿ��ÿ�츶����
�˰�æ��ÿ��ÿ�츶����![]() Ԫ��ũ�ó��˷Ѽ���������˰��ƽ��ÿ��
Ԫ��ũ�ó��˷Ѽ���������˰��ƽ��ÿ��![]() Ԫ��
Ԫ��
![]() �ֱ��ú�
�ֱ��ú�![]() ��
��![]() �Ĵ���ʽ��ʾ���ַ�ʽ����ˮ�������룮
�Ĵ���ʽ��ʾ���ַ�ʽ����ˮ�������룮
![]() ��
��![]() Ԫ��
Ԫ��![]() Ԫ�������ֳ���ˮ����ʽ������ͬ��ʱ��������ȫ��ˮ��������ͨ������˵��ѡ�����ֳ��۷�ʽ�Ϻã�
Ԫ�������ֳ���ˮ����ʽ������ͬ��ʱ��������ȫ��ˮ��������ͨ������˵��ѡ�����ֳ��۷�ʽ�Ϻã�
![]() ��ũ����ǿ�����������������괿����ﵽ
��ũ����ǿ�����������������괿����ﵽ![]() Ԫ�����Ҹ�ũ��������
Ԫ�����Ҹ�ũ��������![]() �нϺõij��۷�ʽ���ۣ���ô�������������Ƕ��٣�������
�нϺõij��۷�ʽ���ۣ���ô�������������Ƕ��٣�������![]() ������-��֧������
������-��֧������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AD=2AB��F��AD���е㣬��CE��AB������E���߶�AB�ϣ�E����A��B�غϣ�������EF��CF�������н�����һ���������� ( )
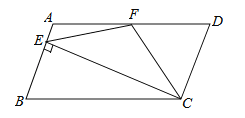
�١�DCF=![]() ��BCD����EF=CF����
��BCD����EF=CF����![]() ���ܡ�DFE=4��AEF��
���ܡ�DFE=4��AEF��
A. �٢ڢۢ� B. �٢ڢ� C. �٢� D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
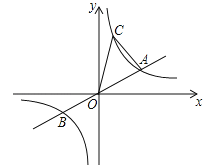
����Ŀ����ͼ,��֪:ֱ��![]() ��˫����
��˫����![]() ����A.B���㣬�ҵ�A�ĺ�����Ϊ4, ��˫����
����A.B���㣬�ҵ�A�ĺ�����Ϊ4, ��˫����![]() ��һ��C��������Ϊ8������AC.
��һ��C��������Ϊ8������AC.
(1)���: k��ֵΪ_______; ��B������Ϊ___________;��C������Ϊ___________.
(2)ֱ��д�����ڵIJ���ʽ![]() �Ľ⼯.
�Ľ⼯.
(3)��������AOC�����
(4) ����x�����е�M��y�����е�N���ҵ�M.N.A.C�ĵ�ǡ�ù���ƽ���ı��Σ�ֱ��д����M.N������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������Ϫˮ��ľ���ˮλ��![]() ����������Ϫˮ����������·�ij�ܼ���ˮλ�仯���������ĩǡ�ôﵽ����ˮλ��������ʾ��ǰһ��ˮλ�ߣ�������ʾ��ǰһ��ˮλ�ͣ���
����������Ϫˮ����������·�ij�ܼ���ˮλ�仯���������ĩǡ�ôﵽ����ˮλ��������ʾ��ǰһ��ˮλ�ߣ�������ʾ��ǰһ��ˮλ�ͣ���
���� | һ | �� | �� | �� | �� | �� | �� |
ˮλ�仯 |
|
|
|
|
|
|
|

![]() �����ĵ�ˮλ�Ƕ��٣�
�����ĵ�ˮλ�Ƕ��٣�
![]() ������һ�����������ˮλ����ߵģ�
������һ�����������ˮλ����ߵģ�
![]() �Ծ���ˮλΪ��㣬������ͼ����ʾ����ˮλ�����
�Ծ���ˮλΪ��㣬������ͼ����ʾ����ˮλ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
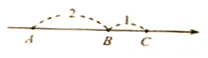
����Ŀ����һ���������������ϴ������е�A��B��C������AB=2��BC=1����ͼ��ʾ�� ���A��B��C����Ӧ���ĺ���p��
��1������BΪԭ�㣬���A��C����Ӧ����Ϊ �� ��p��ֵΪ ������CΪԭ�㣬p ��ֵΪ ��
��2����ԭ��O��ͼ�������ϵ�C���ұߣ���CO=28����p��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�BFƽ�֡�ABC����AD�ڵ�F��CEƽ�֡�BCD����AD�ڵ�E��AB=6��EF=2����BC��Ϊ�� ��

A. 10 B. 8 C. 14 D. 12
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com