
【题目】已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上,若将正方形AEFG绕点A按顺时针方向旋转,连接DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长度始终相等?并说明理由.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】(1)在直角坐标系中描出下列各点A(2,1),B(-2,1),C(3,2),D(-3,2);
(2)连结AB、CD观察它们与y轴的关系,
(3)猜想(a,1)(-a,1)两点的连线是否遵循上述规律.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图数在线的A、B、C三点所表示的数分别为a、b、c.根据图中各点位置,判断下列各式何者正确( )
![]()
A. (a﹣1)(b﹣1)>0 B. (b﹣1)(c﹣1)>0 C. (a+1)(b+1)<0 D. (b+1)(c+1)<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级七班“数学兴趣小组”对函数的对称变换进行探究,以下是探究发现运用过程,请补充完整.
(1)操作发现,在作函数y=|x|的图象时,采用了分段函数的办法,该函数转化为y= ![]() ,请在如图1所示的平面直角坐标系中作出函数的图象;
,请在如图1所示的平面直角坐标系中作出函数的图象;
(2)类比探究
作函数y=|x﹣1|的图象,可以转化为分段函数 , 然后分别作出两段函数的图象.聪明的小昕,利用坐标平面上的轴对称知识,把函数y=x﹣1在x轴下面部分,沿x轴进行翻折,与x轴上及上面部分组成了函数y=|x﹣1|的图象,如图所示;
(3)拓展提高
如图2右图是函数y=x2﹣2x﹣3的图象,请在原坐标系作函数y=|x2﹣2x﹣3|的图象;
(4)实际运用
①函数 ![]() 的图象与x轴有个交点,对应方程|x2﹣2x﹣3|=0有个实根;
的图象与x轴有个交点,对应方程|x2﹣2x﹣3|=0有个实根;
②函数 ![]() 的图象与直线y=5有个交点,对应方程|x2﹣2x﹣3|=5有个实根;
的图象与直线y=5有个交点,对应方程|x2﹣2x﹣3|=5有个实根;
③函数 ![]() 的图象与直线y=4有个交点,对应方程
的图象与直线y=4有个交点,对应方程 ![]() 有个实根;
有个实根;
④关于x的方程 ![]() 有4个实根时,a的取值范围是 .
有4个实根时,a的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列判断错误的是( )

A. 如果∠2=∠4,那么AB∥CD B. 如果∠1=∠3,那么AB∥CD
C. 如果∠BAD+∠D=180°,那么AB∥CD D. 如果∠BAD+∠B=180,那么AD∥CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,连接BQ.若PA=6,PB=8,PC=10,则四边形APBQ的面积为 . 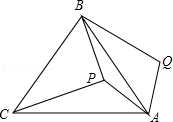
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,一张四边形纸片ABCD,∠A=50°,∠C=150°.若将其按照图②所示方式折叠后,恰好MD′∥AB,ND′∥BC,则∠D的度数为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( )
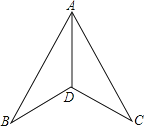
A. BD=DC,AB=AC B. ∠B=∠C,BD=DC
C. ∠B=∠C,∠BAD=∠CAD D. ∠ADB=∠ADC,BD=DC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com