
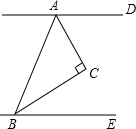
 如图,直线AD∥BE,AC、BC分别平分∠BAD、∠ABE,∠CAD=55°,则∠CBE=35°.
如图,直线AD∥BE,AC、BC分别平分∠BAD、∠ABE,∠CAD=55°,则∠CBE=35°. 分析 先根据角平分线的性质得出∠CAD=$\frac{1}{2}$∠DAB,∠CBE=$\frac{1}{2}$∠ABE,再由平行线的性质即可得出结论.
解答 解:∵AC、BC分别平分∠BAD、∠ABE,
∴∠CAD=$\frac{1}{2}$∠DAB,∠CBE=$\frac{1}{2}$∠ABE.
∵∠CAD=55°,
∴∠DAB=110°.
∵直线AD∥BE,
∴∠ABC=180°-∠DAB=180°-110°=70°,
∴∠CBE=$\frac{1}{2}$∠ABE=$\frac{1}{2}$×70°=35°.
故答案为:35.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,同旁内角互补.


科目:初中数学 来源: 题型:解答题
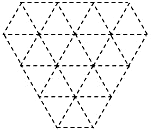 根据题意作出图形,并回答相关问题:请在网格中设计一个图案(图中每个小三角形都是边长为 1的等边三角形),要求所设计的图案既是轴对称图形,又是中心对称图形,并且图案的顶点在格点上,面积等于3$\sqrt{3}$.请将你所设计的图案用铅笔涂黑.
根据题意作出图形,并回答相关问题:请在网格中设计一个图案(图中每个小三角形都是边长为 1的等边三角形),要求所设计的图案既是轴对称图形,又是中心对称图形,并且图案的顶点在格点上,面积等于3$\sqrt{3}$.请将你所设计的图案用铅笔涂黑.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
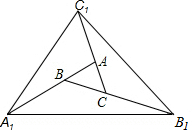 如图,对面积为1的△ABC逐次进行以下操作:第一次操作,分别延长AB、BC、CA至点A1、B1、C1,使得A1B=2AB,B1C=2BC,C1A=2CA,顺次连接A1、B1、C1,得到△A1B1C1,记其面积为S1;第二次操作,分别延长A1B1、B1C1、C1A1至点A2、B2、C2,使得A2B1=2A1B1,B2C1=2B1C1,C2A1=2C1A1,顺次连接A2、B2、C2,得到△A2B2C2,记其面积为S2;按此规律继续下去,可得到△AnBnCn,记其面积为Sn.则S1=19,Sn=19n.
如图,对面积为1的△ABC逐次进行以下操作:第一次操作,分别延长AB、BC、CA至点A1、B1、C1,使得A1B=2AB,B1C=2BC,C1A=2CA,顺次连接A1、B1、C1,得到△A1B1C1,记其面积为S1;第二次操作,分别延长A1B1、B1C1、C1A1至点A2、B2、C2,使得A2B1=2A1B1,B2C1=2B1C1,C2A1=2C1A1,顺次连接A2、B2、C2,得到△A2B2C2,记其面积为S2;按此规律继续下去,可得到△AnBnCn,记其面积为Sn.则S1=19,Sn=19n.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,抛物线y=x2+mx+n经过点A(0,-1),B(3,2)
如图,在平面直角坐标系xOy中,抛物线y=x2+mx+n经过点A(0,-1),B(3,2)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com