
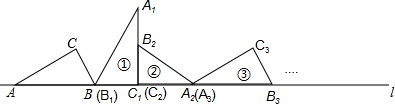
分析 先根据勾股定理计算出AB=2,再根据旋转的性质得到转动3次时BB3等于三角形的周长,接着利用2013=3×671可计算出BB2013的长度,然后加上AB即可得到AB2013.
解答 解:在Rt△ABC中,∵BC=1,AC=$\sqrt{3}$,
∴AB=$\sqrt{{1}^{2}+(\sqrt{3})^{2}}$=2,
∵Rt△ABC在直线l上顺时针方向转动,
当转动3次时,BB3=1+$\sqrt{3}$+2=3+$\sqrt{3}$,
而2013=3×671,
∴当转动2013次时,BB2013=671×(3+$\sqrt{3}$)=2013+671$\sqrt{3}$,
∴AB2013=2015+671$\sqrt{3}$.
故答案为2015+671$\sqrt{3}$.
点评 本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.


科目:初中数学 来源: 题型:解答题
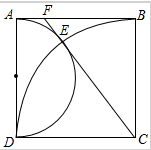 如图,在边长为4的正方形ABCD中,以AD为直径的⊙O,以C为圆心的圆弧BD,与⊙O交于点E,连接CE,并延长交AB于点F.
如图,在边长为4的正方形ABCD中,以AD为直径的⊙O,以C为圆心的圆弧BD,与⊙O交于点E,连接CE,并延长交AB于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
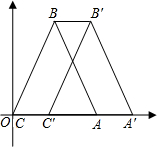 如图,在平面直角坐标系中,△ABC是等腰三角形,BC=BA,B点坐标为(1,$\sqrt{3}$),C点坐标为(0,0),且S△ABC=$\sqrt{3}$.将△ABC沿x轴向右平移$\sqrt{2}$个单位长,使点A、B、C分别平移到A′,B′,C′.
如图,在平面直角坐标系中,△ABC是等腰三角形,BC=BA,B点坐标为(1,$\sqrt{3}$),C点坐标为(0,0),且S△ABC=$\sqrt{3}$.将△ABC沿x轴向右平移$\sqrt{2}$个单位长,使点A、B、C分别平移到A′,B′,C′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在矩形ABCD中,AB=3米,BC=4米,动点P以2米/秒的速度从点A出发,沿AC向点C移动,同时动点Q以1米/秒的速度从点C出发,沿CB向点B移动,设P、Q两点同时移动的时间为t秒(0<t<2.5).
在矩形ABCD中,AB=3米,BC=4米,动点P以2米/秒的速度从点A出发,沿AC向点C移动,同时动点Q以1米/秒的速度从点C出发,沿CB向点B移动,设P、Q两点同时移动的时间为t秒(0<t<2.5).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
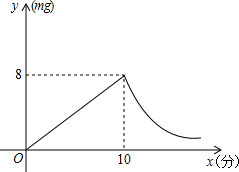 为预防“手足口病”,某校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(分钟)成正比例;燃烧后,y与x成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题:
为预防“手足口病”,某校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(分钟)成正比例;燃烧后,y与x成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点C在线段AB上,AC=6cm,MB=10cm,点M、N分别为AC、BC的中点.
如图,点C在线段AB上,AC=6cm,MB=10cm,点M、N分别为AC、BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com