
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,将点A向右平移6个单位长度,得到点B.
,将点A向右平移6个单位长度,得到点B.
(1)直接写出点B的坐标;
(2)若抛物线y=-x2+bx+c经过点A,B,求抛物线的表达式;
(3)若抛物线y=-x2+bx+c的顶点在直线y=x+2上移动,当抛物线与线段AB有且只有一个公共点时,求抛物线顶点横坐标![]() 的取值范围.
的取值范围.
科目:初中数学 来源: 题型:
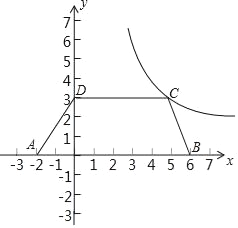
【题目】如图,在四边形ABCD中,CD∥AB,AD=BC.已知A(﹣2,0),B(6,0),D(0,3),函数y=![]() (x>0)的图象G经过点C.
(x>0)的图象G经过点C.
(1)求点C的坐标和函数y=![]() (x>0)的表达式;
(x>0)的表达式;
(2)将四边形ABCD向上平移2个单位得到四边形A'B'C'D',问点B'是否落在图象G上?
查看答案和解析>>
科目:初中数学 来源: 题型:
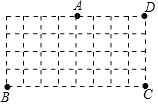
【题目】如图是由边长为1的小正方形组成的8×4网格,每个小正方形的顶点叫做格点,点A,B,C,D均在格点上,在网格中将点D按下列步骤移动:
第一步:点D绕点A顺时针旋转180°得到点D1;
第二步:点D1绕点B顺时针旋转90°得到点D2;
第三步:点D2绕点C顺时针旋转90°回到点D.
(1)请用圆规画出点D→D1→D2→D经过的路径;
(2)所画图形是什么对称图形;
(3)求所画图形的周长(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
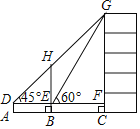
【题目】如图,某数学兴趣小组为测量一棵古树BH和教学楼CG的高,先在A处用高1.5米的测角仪测得古树顶端H的仰角∠HDE为45°,此时教学楼顶端G恰好在视线DH上,再向前走7米到达B处,又测得教学楼顶端G的仰角∠GEF为60°,点A、B、C三点在同一水平线上.
(1)计算古树BH的高;
(2)计算教学楼CG的高.(参考数据:![]() ≈14,
≈14,![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小西“过直线外一点作这条直线的垂线”的尺规作图过程.
已知:直线l及直线l外一点P.
求作:直线PQ,使得PQ⊥l.
做法:如图,
①在直线l的异侧取一点K,以点P为圆心,PK长为半径画弧,交直线l于点A,B;
②分别以点A,B为圆心,大于![]() AB的同样长为半径画弧,两弧交于点Q(与P点不重合);
AB的同样长为半径画弧,两弧交于点Q(与P点不重合);
③作直线PQ,则直线PQ就是所求作的直线.
根据小西设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵PA= ,QA= ,
∴PQ⊥l( )(填推理的依据).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2-4x+c(a≠0)与反比例函数y=![]() 的图象相交于B点,且B点的横坐标为3,抛物线与y轴交于点C(0,6),A是抛物线y=ax2-4x+c的顶点,P点是x轴上一动点,当PA+PB最小时,P点的坐标为_______.
的图象相交于B点,且B点的横坐标为3,抛物线与y轴交于点C(0,6),A是抛物线y=ax2-4x+c的顶点,P点是x轴上一动点,当PA+PB最小时,P点的坐标为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明设计的“作平行四边形的高”的尺规作图过程
已知:平行四边形ABCD.
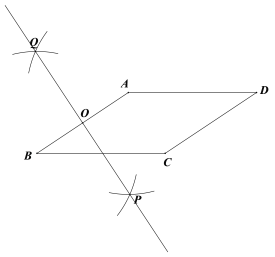
求作:![]() ,垂足为点E.
,垂足为点E.
作法:如图,
①分别以点A和点B为圆心,大于![]() 的长为半径作弧,两弧相交于P,Q两点;
的长为半径作弧,两弧相交于P,Q两点;
②作直线PQ,交AB于点O;
③以点O为圆心,OA长为半径做圆,交线段BC于点E;
④连接AE.
所以线段AE就是所求作的高.
根据小明设计的尺规作图过程
⑴使用直尺和圆规,补全图形;(保留作图痕迹)
⑵完成下面的证明
证明:![]() AP=BP, AQ= ,
AP=BP, AQ= ,
![]() PQ为线段AB的垂直平分线.
PQ为线段AB的垂直平分线.
![]() O为AB中点.
O为AB中点.
![]() AB为直径,⊙O与线段BC交于点E,
AB为直径,⊙O与线段BC交于点E,
![]()
![]()
![]() .( )(填推理的依据)
.( )(填推理的依据)
![]()
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有大小两种货车,3辆大货车与4辆小货车一次可以运货18吨,2辆大货车与6辆小货车一次可以运货17吨.
(1)请问1辆大货车和1辆小货车一次可以分别运货多少吨?
(2)目前有33吨货物需要运输,货运公司拟安排大小货车共计10辆,全部货物一次运完,其中每辆大货车一次运费花费130元,每辆小货车一次运货花费100元,请问货运公司应如何安排车辆最节省费用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,AC是⊙O的直径,OB是⊙O的半径,PA切⊙O于点A,PB与AC的延长线交于点M,∠COB=∠APB.
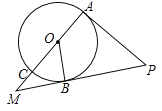
(1)求证:PB是⊙O的切线;
(2)当OB=3,PA=6时,求MB,MC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com