
【题目】在达州市关工委组织的“五好小公民”主题教育活动中,我市某中学组织全校学生参加了“红旗队飘,引我成长”知识竞赛,赛后机抽取了部分参赛学生的成绩,从高分到低分将成绩分成![]() 五类,绘制成下面两个不完整的统计图:
五类,绘制成下面两个不完整的统计图:
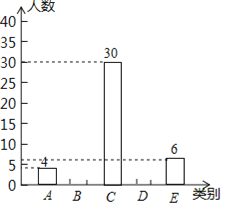
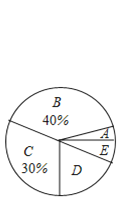
根据上面提供的信息解答下列问题:
(1)补全条形统计图;
(2)若该校共有学生4200人,求成绩为![]() 类的学生人数和
类的学生人数和![]() 类学生所对应的圆心角的度数;
类学生所对应的圆心角的度数;
(3)若![]() 类恰好是2名男生和2名女生,随机选择2名学生担任校园广播“孝心伴我行”节目主持人,请用列表法或画树状图法求恰好抽到1名男生和1名女生的概率.
类恰好是2名男生和2名女生,随机选择2名学生担任校园广播“孝心伴我行”节目主持人,请用列表法或画树状图法求恰好抽到1名男生和1名女生的概率.
【答案】(1)图详见解析;(2)840,72°;(3)![]()
【解析】
(1)首先用C类别的学生人数除以C类别的人数占的百分率,求出共调查多少名学生;然后根据B类别百分比求得其人数,由各类别人数和等于总人数求得D的人数,即可补全统计图;
(2)用全校人数乘以D类别人数所占比例即可得到成绩为![]() 类的学生人数,用360
类的学生人数,用360![]() 乘以样本中D类别人数所占比例可得其圆心角度数;
乘以样本中D类别人数所占比例可得其圆心角度数;
(3)若A等级的4名学生中有2名男生2名女生,现从中任意选取2名担任校园广播“孝心伴我行”节目主持人,应用列表法的方法,求出恰好选到1名男生和1名女生的概率是多少即可.
解:(1)∵被调查的总人数为30÷30%=100人,则B类别人数为100×40%=40人,
∴D类别人数为100﹣(4+40+30+6)=20人,
补全条形图如下:
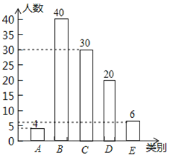
(2)D类的学生人数:4200×(20÷100)=840(人),
D类所对应的圆心角是![]()
(3)列表为:
男1 | 男2 | 女1 | 女2 | |
男1 | ﹣﹣ | 男2男1 | 女1男1 | 女2男1 |
男2 | 男1男2 | ﹣﹣ | 女1男2 | 女2男2 |
女1 | 男1女1 | 男2女1 | ﹣﹣ | 女2女1 |
女2 | 男1女2 | 男2女2 | 女1女2 | ﹣﹣ |
由上表可知,从4名学生中任意选取2名学生共有12种等可能结果,其中恰好选到1名男生和1名女生的结果有8种,
∴恰好选到1名男生和1名女生的概率为![]() .
.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案科目:初中数学 来源: 题型:
【题目】央视举办的《主持人大赛》受到广泛的关注.某中学学生会就《主持人大赛》节目的喜爱程度,在校内对部分学生进行了问卷调查,并对问卷调查的结果分为“非常喜欢”、“比较喜欢”、“感觉一般”、“不太喜欢”四个等级,分别记作![]() 、
、![]() 、
、![]() 、
、![]() .根据调查结果绘制出如图所示的扇形统计图和条形统计图,请结合图中所给信息解答下列问题:
.根据调查结果绘制出如图所示的扇形统计图和条形统计图,请结合图中所给信息解答下列问题:
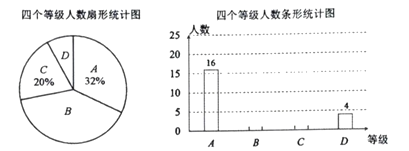
(1)本次被调查对象共有 人;扇形统计图中被调查者“比较喜欢”等级所对应圆心角的度数为 .
(2)将条形统计图补充完整,并标明数据;
(3)若选“不太喜欢”的人中有两个女生和两个男生,从选“不太喜欢”的人中挑选两个学生了解不太喜欢的原因,请用列举法(画树状图或列表),求所选取的这两名学生恰好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
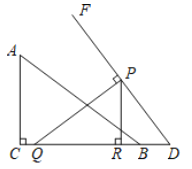
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 在边
在边![]() 的延长线上,且
的延长线上,且![]() .在
.在![]() 上方作射线
上方作射线![]() ,使
,使![]() .点
.点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度,沿射线
出发,以每秒1个单位长度的速度,沿射线![]() 方向运动.过点
方向运动.过点![]() 作
作![]() ,垂足为
,垂足为![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,交线段
,交线段![]() 或线段
或线段![]() 于点
于点![]() ,当点
,当点![]() 与点
与点![]() 重合时,点
重合时,点![]() 停止运动.设点
停止运动.设点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
(1)线段![]() 的长为______.(用含
的长为______.(用含![]() 的代数式表示)
的代数式表示)
(2)当点![]() 与点
与点![]() 重合时,求
重合时,求![]() 的值.
的值.
(3)设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(4)当点![]() 在
在![]() 的某一条边的中垂线上时,直接写出
的某一条边的中垂线上时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
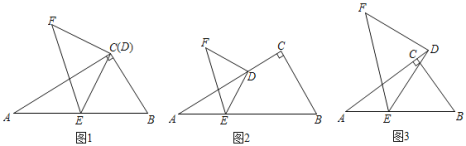
【题目】观察猜想:
(1)如图1,在Rt△ABC中,∠ACB=90°,∠BAC=30°,点D与点C重合,点E在斜边AB上,连接DE,且DE=AE,将线段DE绕点D顺时针旋转90°得到线段DF,连接EF,则![]() =______,sin∠ADE=________,
=______,sin∠ADE=________,
探究证明:
(2)在(1)中,如果将点D沿CA方向移动,使CD=![]() AC,其余条件不变,如图2,上述结论是否保持不变?若改变,请求出具体数值:若不变,请说明理由.
AC,其余条件不变,如图2,上述结论是否保持不变?若改变,请求出具体数值:若不变,请说明理由.
拓展延伸
(3)如图3,在△ABC中,∠ACB=90°,∠CAB=a,点D在边AC的延长线上,E是AB上任意一点,连接DE.ED=nAE,将线段DE绕着点D顺时针旋转90°至点F,连接EF.求![]() 和sin∠ADE的值分别是多少?(请用含有n,a的式子表示)
和sin∠ADE的值分别是多少?(请用含有n,a的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=x+4的图象与反比例函数y=![]() (k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求此反比例函数的表达式;
(2)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标.
S△BOC,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
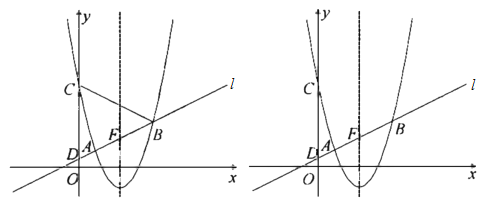
【题目】如图,在平面直角坐标系![]() 中,以直线
中,以直线![]() 为对称轴的抛物线
为对称轴的抛物线![]() 与直线
与直线![]() 交于
交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于
轴交于![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线的函数表达式;
(2)设直线![]() 与抛物线的对称轴的交点为
与抛物线的对称轴的交点为![]() ,
,![]() 是抛物线上位于对称轴右侧的一点,若
是抛物线上位于对称轴右侧的一点,若![]() ,且
,且![]() 与
与![]() 的面积相等,求点
的面积相等,求点![]() 的坐标;
的坐标;
(3)若在![]() 轴上有且只有一点
轴上有且只有一点![]() ,使
,使![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了改善教室空气环境,某校九年级1班班委会计划到朝阳花卉基地购买绿植.已知该基地一盆绿萝与一盆吊兰的价格之和是12元.班委会决定用60元购买绿萝,用90元购买吊兰,所购绿萝数量正好是吊兰数量的两倍.
(1)分别求出每盆绿萝和每盆吊兰的价格;
(2)该校九年级所有班级准备一起到该基地购买绿萝和吊兰共计90盆,其中绿萝数量不超过吊兰数量的一半,该基地特地对吊兰价格给出了如下的优惠政策,一次性购买的吊兰超过20盆时,超过部分的吊兰每盆的价格打8折,根据该基地的优惠信息,九年级购买这两种绿植各多少盆时总费用最少?最少费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某人在山坡坡脚![]() 处测得一座建筑物顶点
处测得一座建筑物顶点![]() 的仰角为
的仰角为![]() ,沿山坡向上走到
,沿山坡向上走到![]() 处再测得该建筑物顶点
处再测得该建筑物顶点![]() 的仰角为
的仰角为![]() .已知
.已知![]() 米,
米,![]() ,
,![]() 的延长线交于点
的延长线交于点![]() ,山坡坡度为
,山坡坡度为![]() (即
(即![]() ).注:取
).注:取![]() 为
为![]() .
.
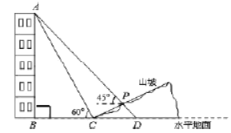
(1)求该建筑物的高度(即![]() 的长).
的长).
(2)求此人所在位置点![]() 的铅直高度(测倾器的高度忽略不计).
的铅直高度(测倾器的高度忽略不计).
(3)若某一时刻,![]() 米长木棒竖放时,在太阳光线下的水平影长是
米长木棒竖放时,在太阳光线下的水平影长是![]() 米,则同一时刻该座建筑物顶点
米,则同一时刻该座建筑物顶点![]() 投影与山坡上点
投影与山坡上点![]() 重合,求点
重合,求点![]() 到该座建筑物的水平距离.
到该座建筑物的水平距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅行社推出一条成本价为500元/人的省内旅游线路.游客人数![]() (人/月)与旅游报价
(人/月)与旅游报价![]() (元/人)之间的关系为
(元/人)之间的关系为![]() ,已知:旅游主管部门规定该旅游线路报价在800元/人~1200元/人之间.
,已知:旅游主管部门规定该旅游线路报价在800元/人~1200元/人之间.
(1)要将该旅游线路每月游客人数控制在200人以内,求该旅游线路报价的取值范围;
(2)求经营这条旅游线路每月所需要的最低成本;
(3)当这条旅游线路的旅游报价为多少时,可获得最大利润?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com