练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

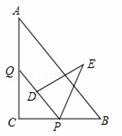
    如图，Rt△ABC中，∠C=90°，AB=15，BC=9，点P，Q分别在BC，AC上，CP=3x，CQ=4x（0＜x＜3）．把△PCQ绕点P旋转，得到△PDE，点D落在线段PQ上．

    （1）求证：PQ∥AB；（2）若点D在∠BAC的平分线上，求CP的长；

     


    解：（1）证明：∵在Rt△ABC中，AB=15，BC=9，∴．

    ∵，∴．又∵∠C=∠C，∴△PQC∽△BAC.∴∠CPQ=∠B. ∴PQ∥AB.

    （2）如答图1，连接AD，∵PQ∥AB，∴∠ADQ=∠DAB．∵点D在∠BAC的平分线上，∴∠DAQ=∠DAB.∴∠ADQ=∠DAQ. ∴AQ=DQ．在Rt△CPQ中，∵CP=3x，CQ=4x，∴PQ=5x.∵PD=PC=3x，∴DQ=2x．∵AQ=12﹣4x，∴12﹣4x=2x，解得x=2.∴CP=3x=6．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    若等腰三角形的周长为26cm，一边为11cm，则腰长为（    ）

      A．11㎝        B．7.5㎝      C．11㎝ 或7.5㎝     D．以上都不对

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知Rt△ABC的两直角边的长分别为6cm和8cm，则它的外接圆的半径为　　cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知a是方程x2＋x－2015＝0的一个根，则的值为（     ）

       A．2014         B．2015        C．          D．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


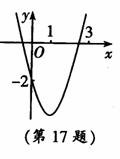
    如图，已知抛物线y＝x2＋bx＋c经过点（0，－2），请你确定

    一个b的值，使该抛物线与x轴的一个交点在(1，0)和(3，0)之间．

    你所确定的b的值为         ．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知关于x的方程x2－(k＋2)x＋2k＝0．

    (1)求证：k取任何实数值，方程总有实数根；

    (2)若等腰△ABC的一边长a＝3，另两边长b，c恰好是这个方程的两个根，求△ABC的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    直接写出下列各式分解因式的结果

    x（y－x）－y（x－y）=__________．  

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    给出下列条件： ①两边一角对应相等　②两角一边对应相等　③三角形中三角对应相等　④三边对应相等，其中，不能使两个三角形全等的条件是（   ）

    A．①③             B．①②             C．②③             D．②④

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，该图形绕点O按下列角度旋转后，不能与其自身重合的是(     )

    A．72°   B．108°  C．144°  D．216°

    查看答案和解析>>

    同步练习册答案