
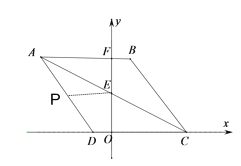
【题目】如图,O为坐标原点,四边形ABCD是菱形,A(-4,4),B点在第一象限,AB=5,AB与y轴交于点F,对角线AC交y轴于点E.
(1)直接写出B点C点坐标;
(2)动点P从C点出发以每秒1个单位的速度沿折线段C—D—A运动,求△EDP的面积y与时间t的关系式
(3)在(2)的条件下,是否存在一点P,使△APE沿其一边翻折构成的四边形是菱形,若存在,求出点P坐标;若不存在,请说明理由.


【答案】(1)B(1,4),C(4,0);(2)y=5-t(0≤t<5),y=t-5(5<t≤10);(3)存在,P(-2.5,2)或P(![]() -4,
-4,![]() )
)
【解析】
(1)根据A点坐标和AB=5可得B点坐标,过点B作BG⊥OC,求出GC即可得到C点坐标;
(2)过点E作EN⊥BC于点N,延长EN交AD于M,所以MN⊥AD,根据菱形的性质可得OE=EN,OC=CN=4,在Rt△BNE和Rt△BFE中,通过勾股定理构建方程求出OE=EF=ME=2,然后根据三角形面积公式列式即可;
(3)分两种情况:①点P在DA上,且AP=AE时,沿PE翻折,可得四边形为菱形,此时可根据相似三角形的性质求出PR,DR,从而得到P点坐标;②当P在DA上,且AP=PE时,沿AE翻折,可得四边形为菱形,此时PE为△ADC的中位线,根据中点坐标公式可求出P点坐标.
解:(1)∵A(-4,4),AB=5,四边形ABCD是菱形,
∴B (1,4),BF=1,
过点B作BG⊥OC,则BG=4,BC=5,
∴GC=3,
∴C(4,0)
(2)过点E作EN⊥BC于点N,延长EN交AD于M,所以MN⊥AD,
∵四边形ABCD是菱形,∴∠DCA=∠BCA,
∴OE=EN,
由(1)知OC=4,∴CN=4,BN=1,
设OE=x,则OE=EN=x,EF=4-x,
在Rt△BNE中,BE2=x2+1,在Rt△BFE中,BE2=(4-x)2+1,
∴x2+1=(4-x)2+1,解得:x=2,即OE=2,EF=2,
∴ME=EF=2,
∴当点P在CD上时,y=![]() ,
,
当点P在DA上时,y=![]() ,
,
(3)①如图:点P在DA上,且AP=AE时,沿PE翻折,可得四边形为菱形,
作AQ⊥OQ,PR⊥OQ,由(1)(2)可得OD=1,EF=2,AF=4,
根据勾股定理可得:AP=AE=![]() ,∴PD=5-
,∴PD=5-![]() ,
,
易得△PRD∽△AQD,∴![]() ,
,
∴PR=4-![]() ,DR=3-
,DR=3-![]() ,∴OR=4-
,∴OR=4-![]() ,
,
∴此时P点坐标为(![]() );
);

②如图:当P在DA上,且AP=PE时,沿AE翻折,可得四边形为菱形,
∵AP=PE,∴∠PAE=∠PEA,
又∵∠PAE=∠EAF,
∴∠PEA=∠EAF,
∴AF∥PE∥CD,
由(1)(2)可知E为AC中点,∴P为AD中点,
∵A(-4,4),D(-1,0),
∴P(![]() )
)
综上所述:满足题意的P点坐标为(![]() )或(
)或(![]() ).
).


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】泰兴出租车司机小李某天下午的营运全是在东西走向的国庆路上进行的,若规定向东为正,向西为负,这天下午的行车里程如下(单位:千米):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:千米).
(单位:千米).
(1)将最后一名乘客送到目的地后,小李距下午出发地点的距离是多少千米?
(2)若出租车每行驶![]() 耗油
耗油![]() ,这天下午这辆出租车共消耗多少升汽油?
,这天下午这辆出租车共消耗多少升汽油?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,□ABCD的顶点坐标分别为A(3.6,a),B(2,2),C(b,3.4),D(8,6),则![]() 的值为( )
的值为( )

A. 8 B. 9 C. 10 D. 11
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个三位正整数t,将各数位上的数字重新排序后(包括本身),得到一个新的三位数![]() (a≤c),在所有重新排列的三位数中,当|a+c﹣2b|最小时,称此时的
(a≤c),在所有重新排列的三位数中,当|a+c﹣2b|最小时,称此时的 ![]() 为t的“最优组合”,并规定F(t)=|a﹣b|﹣|b﹣c|,例如:124重新排序后为:142、214、因为|1+4﹣4|=1,|1+2﹣8|=5,|2+4﹣2|=4,所以124为124的“最优组合”,此时F(124)=﹣1.
为t的“最优组合”,并规定F(t)=|a﹣b|﹣|b﹣c|,例如:124重新排序后为:142、214、因为|1+4﹣4|=1,|1+2﹣8|=5,|2+4﹣2|=4,所以124为124的“最优组合”,此时F(124)=﹣1.
(1)三位正整数t中,有一个数位上的数字是另外两数位上的数字的平均数,求证:F(t)=0;
(2)一个正整数,由N个数字组成,若从左向右它的第一位数能被1整除,它的前两位数能被2整除,前三位数能被3整除,…,一直到前N位数能被N整除,我们称这样的数为“善雅数”.例如:123的第一位数1能披1整除,它的前两位数12能被2整除,前三位数123能被3整除,则123是一个“善雅数”.若三位“善雅数”m=200+10x+y(0≤x≤9,0≤y≤9,x、y为整数),m的各位数字之和为一个完全平方数,求出所有符合条件的“善雅数”中F(m)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度![]() (单位:
(单位:![]() )与足球被踢出后经过的时间
)与足球被踢出后经过的时间![]() (单位:
(单位:![]() )之间的关系如下表:
)之间的关系如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| 0 | 8 | 14 | 18 | 20 | 20 | 18 | 14 | … |
下列结论:①足球距离地面的最大高度为![]() ;②足球飞行路线的对称轴是直线
;②足球飞行路线的对称轴是直线![]() ;③足球被踢出
;③足球被踢出![]() 时落地;④足球被踢出
时落地;④足球被踢出![]() 时,距离地面的高度是
时,距离地面的高度是![]() .
.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场在“双十一”促销活动中决定对购买空调的顾客实行现金返利.规定每购买一台空调,商场返利若干元.经调查,销售空调数量y1(单位:台)与返利x(单位:元)之间的函数表达式为![]() .每台空调的利润y2(单位:元)与返利x的函数图像如图所示.
.每台空调的利润y2(单位:元)与返利x的函数图像如图所示.
(1)求y2与x之间的函数表达式;

(2)每台空调返利多少元才能使销售空调的总利润最大?最大总利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的轨道上有两个点甲与乙,开始时甲在A处,乙在C处,它们沿着正方形轨道顺时针同时出发,甲的速度为每秒1 cm,乙的速度为每秒5 cm,已知正方形轨道ABCD的边长为2 cm,则乙在第2 020次追上甲时的位置在( )

A.AB上B.BC上
C.CD上D.AD上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平直角坐标系xOy中,直线![]() 与反比例函数
与反比例函数![]() 的图象关于点
的图象关于点![]()

(1)求点P的坐标及反比例函数的解析式;
(2)点![]() 是x轴上的一个动点,若
是x轴上的一个动点,若![]() ,直接写出n的取值范围。
,直接写出n的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠的放在一个长为![]() ,宽为
,宽为![]() 的长方形内,该长方形内部未被卡片覆盖的部分用阴影表示.
的长方形内,该长方形内部未被卡片覆盖的部分用阴影表示.

(1)能否用只含![]() 的式子表示出图②中两块阴影部分的周长和?_____(填“能”或“不能”);(2)若能,请你用只含
的式子表示出图②中两块阴影部分的周长和?_____(填“能”或“不能”);(2)若能,请你用只含![]() 的式子表示出中两块阴影部分的周长和;若不能,请说明理由_____.
的式子表示出中两块阴影部分的周长和;若不能,请说明理由_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com