
【题目】如图,正方形ABCD的边长为2,点E是BC的中点,AE与BD交于点P,F是CD上一点,连接AF分别交BD,DE于点M,N且AF⊥DE,连接PN,则以下结论中:①S△ABM=4S△FDM;②PN=![]() ;③tan∠EAF=
;③tan∠EAF=![]() ;④△PMN∽△DPE.正确的是________.(填序号)
;④△PMN∽△DPE.正确的是________.(填序号)
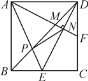
【答案】①②③
【解析】
先证ABM~FDM,利用相似三角形的性质即可判断①;过点P作PH⊥AN于点H,根据平行线分线段成比例定理,求出AP,AH的长,进一步得PH,HN的长,由勾股定理即可求出PN的长,即可判断②;分别求出EN,AN的长,即可判断③;证明∠DPN≠∠PDE,即可判断④.
∵正方形ABCD的边长为2,点E是BC的中点,
∴AB=BC=CD=AD=2,∠ABC=∠C=∠ADF=90°,CE=BE=1,
∵AF⊥DE,
∴∠DAF+∠ADN=∠ADN+∠CDE=90°,
∴∠DAF=∠CDE,
又∵AD=CD,∠ADF=∠DCE=90°,
∴ADFDCE(ASA),
∴DF=CE=1,
∵AB∥DF,
∴ABM~FDM,
∴![]() ,
,
∴S△ABM=4S△FDM,故①正确;
∵AB=CD,BE=CE,∠ABE=∠C=90°,
∴ABEDCE(SAS),
∴AE=DE=AF=![]() ,
,
∵![]() ,
,
∴DN=![]() ,
,
∴EN=DE-DN=![]() -
-![]() =
=![]() ,AN=
,AN=![]() ,
,
∴tan∠EAF=![]() ,故③正确;
,故③正确;
过点P作PH⊥AN于点H,
∵BE∥AD,
∴![]() ,
,
∴PA=![]() ,
,
∵tan∠EAF=![]() ,
,
∴sin∠EAF=![]() ,
,
∴PH=PAsin∠EAF=![]() ,
,
∵PH∥EN,
∴![]() ,
,
∴AH=![]() ,HN=AN-AH=
,HN=AN-AH=![]() ,
,
∴PN=![]() ,故②正确;
,故②正确;
∵PN≠DN,
∴∠DPN≠∠PDE,
∴△PMN与△DPE不相似,故④错误.
故答案是:①②③.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】若抛物线y=x2﹣3x+c与y轴的交点为(0,2),则下列说法正确的是( )
A. 抛物线开口向下
B. 抛物线与x轴的交点为(﹣1,0),(3,0)
C. 当x=1时,y有最大值为0
D. 抛物线的对称轴是直线x=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AC为直径,弧AE=弧BD,BE⊥DC交DC的延长线于点E.
(1)求证:∠1=∠BCE;
(2)求证:BE是⊙O的切线;
(3)若EC=1,CD=3,求cos∠DBA.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】天门山索道是世界最长的高山客运索道,位于张家界天门山景区.在一次检修维护中,检修人员从索道A处开始,沿A﹣B﹣C路线对索道进行检修维护.如图:已知![]() 米,
米,![]() 米,AB与水平线
米,AB与水平线![]() 的夹角是
的夹角是![]() ,BC与水平线
,BC与水平线![]() 的夹角是
的夹角是![]() .求:本次检修中,检修人员上升的垂直高度
.求:本次检修中,检修人员上升的垂直高度![]() 是多少米?(结果精确到1米,参考数据:
是多少米?(结果精确到1米,参考数据:![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,过点O作弦AD的垂线交半圆O于点E,交AC于点C,使∠BED=∠C.
(1)判断直线AC与圆O的位置关系,并证明你的结论;
(2)若AC=8,cos∠BED=![]() ,求AD的长.
,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店准备购进![]() 两种商品,
两种商品,![]() 种商品毎件的进价比
种商品毎件的进价比![]() 种商品每件的进价多20元,用3000元购进
种商品每件的进价多20元,用3000元购进![]() 种商品和用1800元购进
种商品和用1800元购进![]() 种商品的数量相同.商店将
种商品的数量相同.商店将![]() 种商品每件的售价定为80元,
种商品每件的售价定为80元,![]() 种商品每件的售价定为45元.
种商品每件的售价定为45元.
(1)![]() 种商品每件的进价和
种商品每件的进价和![]() 种商品每件的进价各是多少元?
种商品每件的进价各是多少元?
(2)商店计划用不超过1560元的资金购进![]() 两种商品共40件,其中
两种商品共40件,其中![]() 种商品的数量不低于
种商品的数量不低于![]() 种商品数量的一半,该商店有几种进货方案?
种商品数量的一半,该商店有几种进货方案?
(3)端午节期间,商店开展优惠促销活动,决定对每件![]() 种商品售价优惠
种商品售价优惠![]() (
(![]() )元,
)元,![]() 种商品售价不变,在(2)条件下,请设计出销售这40件商品获得总利润最大的进货方案.
种商品售价不变,在(2)条件下,请设计出销售这40件商品获得总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,函数![]() 的图象G经过点
的图象G经过点![]() ,直线
,直线![]() 与y轴交于点B,与图象G交于点C.
与y轴交于点B,与图象G交于点C.
(1)求m的值.
(2)横、纵坐标都是整数的点叫做整点.记图象G在点A,C之间的部分与线段BA,BC围成的区域(不含边界)为W.
①当直线l过点![]() 时,直接写出区域W内的整点个数.
时,直接写出区域W内的整点个数.
②若区域W内的整点不少于4个,结合函数图象,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
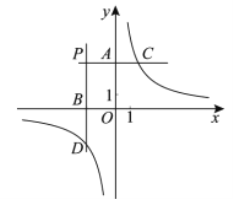
【题目】如图,分别过第二象限内的点![]() 作
作![]() ,
,![]() 轴的平行线,与
轴的平行线,与![]() ,
,![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,与双曲线
,与双曲线![]() 分别交于点
分别交于点![]() ,
,![]() .
.
下面三个结论,
①存在无数个点![]() 使
使![]() ;
;
②存在无数个点![]() 使
使![]() ;
;
③存在无数个点![]() 使
使![]() .
.
所有正确结论的序号是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com