
【题目】如图,已知,BE平分∠ABD,DE平分∠BDC,且∠EBD+∠EDB=90°. 
(1)求证:AB∥CD;
(2)H是直线CD上一动点(不与点D重合),BI平分∠HBD.写出∠EBI与∠BHD的数量关系,并说明理由.
【答案】
(1)证明:∵BE平分∠ABD,DE平分∠BDC,
∴∠ABD=2∠EBD,∠BDC=2∠BDE,
∵∠EBD+∠EDB=90°,
∴∠ABD+∠BDC=2×90°=180°,
∴AB∥CD
(2)解:∵BE平分∠ABD,
∴∠ABD=2∠EBD,
∵BI平分∠HBD,
∴∠HBD=2∠IBD,
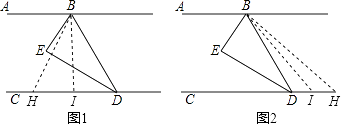
如图1,点H在点D的左边时,∠ABH=∠ABD﹣∠HBD,
∠EBI=∠EBD﹣∠IBD,
∴∠ABH=2∠EBI,
∵AB∥CD,
∴∠BHD=∠ABH,
∴∠BHD=2∠EBI,
如图2,点H在点D的右边时,∠ABH=∠ABD+∠HBD,
∠EBI=∠EBD+∠IBD,
∴∠ABH=2∠EBI,
∵AB∥CD,
∴∠BHD=180°﹣∠ABH,
∴∠BHD=180°﹣2∠EBI,
综上所述,∠BHD=2∠EBI或∠BHD=180°﹣2∠EBI.
【解析】(1)根据角平分线的定义可得∠ABD=2∠EBD,∠BDC=2∠BDE,然后求出∠ABD+∠BDC=180°,再根据同旁内角互补,两直线平行证明;(2)根据角平分线的定义可得∠ABD=2∠EBD,∠HBD=2∠IBD,然后分点H在点D的左边和右边两种情况,表示出∠ABH和∠EBI,从而得解.
【考点精析】根据题目的已知条件,利用平行线的性质的相关知识可以得到问题的答案,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
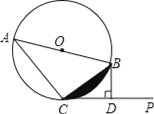
【题目】已知:AB是⊙O的直径,直线CP切⊙O于点C,过点B作BD⊥CP于D.
(1)求证:CB2=ABDB;
(2)若⊙O的半径为2,∠BCP=30°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在全运会射击比赛的选拔赛中,运动员甲10次射击成绩的统计表(表1)和扇形统计图如下:
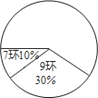
表1
(1)根据统计表(图)中提供的信息,补全统计表及扇形统计图;
(2)已知乙运动员10次射击的平均成绩为9环,方差为1.2,如果只能选一人参加比赛,你认为应该派谁去?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() (
(![]() )的对称轴为直线
)的对称轴为直线![]() ,与x轴的一个交点A在点
,与x轴的一个交点A在点![]() 和
和![]() 之间,其部分图象如图,则下列4个结论:①
之间,其部分图象如图,则下列4个结论:①![]() ;②2a
;②2a![]() b=0;③
b=0;③![]() ;④点M(
;④点M(![]() ,
, ![]() )、N(
)、N(![]() ,
, ![]() )在抛物线上,若
)在抛物线上,若![]() ,
,
则![]() ,其中正确结论的个数是( ).
,其中正确结论的个数是( ).

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果a是b的近似值,那么我们把b叫做a的真值.若用四舍五入法得到的近似数是85,则下列各数不可能是其真值的是( )
A. 85.01 B. 84.51 C. 84.99 D. 84.49
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司员工的月工资如下表:
则这组数据的平均数、众数、中位数分别为( ).
A.2200元、1800元、1600元
B.2000元、1600元、1800元
C.2200元、1600元、1800元
D.1600元、1800元、1900元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三人之间相互传球,球从一个人手中随机传到另外一个人手中,共传球三次.
(1)若开始时球在甲手中,求经过三次传球后,球传回甲手中的概率是多少?
(2)若丙想使球经过三次传递后,球落在自己手中的概率最大,丙会让球开始时在谁手中?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com