
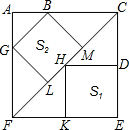
 如图,边长为6的大正方形中有两个小正方形,两个小正方形的面积分别为S1、S2
如图,边长为6的大正方形中有两个小正方形,两个小正方形的面积分别为S1、S2分析 (1)由△FGL和△ABG都为等腰直角三角形,于是得到FL=LG,AB=AG,∠FLG=∠A=90°,求得sin∠GFL=sin45°=$\frac{GL}{GF}$=$\frac{\sqrt{2}}{2}$,即GL=$\sqrt{2}$GL,同理可得:GL=BG=$\sqrt{2}$AB,由于GF=$\sqrt{2}$BG=2AB,又AF=AG+GF=6,即可得到AB=$\frac{6}{3}$=2,由于∠KFH=∠KHF=45°,根据等腰三角形的性质得到FK=KH,根据正方形的性质得到HK=KE,于是得到FK=KE,即可得到结果;
(2)由(1)知AB=2,于是求得S2的面积为BG2=8,由(1)求得DE=3,于是求得S1的面积为3×3=9,即可得到结论.
解答 解:(1)∵△FGL和△ABG都为等腰直角三角形,
∴FL=LG,AB=AG,∠FLG=∠A=90°,
∴sin∠GFL=sin45°=$\frac{GL}{GF}$=$\frac{\sqrt{2}}{2}$,即GL=$\sqrt{2}$GL,同理可得:GL=BG=$\sqrt{2}$AB,
∴GF=$\sqrt{2}$BG=2AB,又AF=AG+GF=6,
∴AB=$\frac{6}{3}$=2,
∵∠KFH=∠KHF=45°,
∴FK=KH,
∵HK=KE,
∴FK=KE,
∴K为EF的中点,
∴DE=3;
(2)由(1)知AB=2,
∴BG2=22+22=8,
∴S2的面积为BG2=8,
由(1)求得DE=3,
∴S1的边长为3,
∴S1的面积为3×3=9,
∴S1+S2=8+9=17.
点评 本题考查了正方形的性质和等腰直角三角形的性质的性质,考查了学生的读图能力和计算能力,题目比较典型,难度适中.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
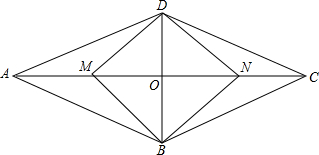 如图,菱形ABCD与矩形BMDN有公共对角线BD,M,N在AC上,且AC=4,BD=2,则AD:DM=$\sqrt{5}$:$\sqrt{2}$.
如图,菱形ABCD与矩形BMDN有公共对角线BD,M,N在AC上,且AC=4,BD=2,则AD:DM=$\sqrt{5}$:$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com