
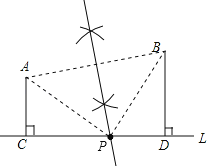
【题目】如图,在笔直的公路L的同侧有A、B两个村庄,已知A、B两村分别到公路的距离AC=3km,BD=4km.现要在公路上建一个汽车站P,使该车站到A、B两村的距离相等,

(1)试用直尺和圆规在图中作出点P;(保留作图痕迹)
(2)若连接AP、BP,测得∠APB=90°,求A村到车站的距离.
【答案】(1)作图见解析;(2)A村到车站的距离5km.
【解析】
试题分析:(1)连接AB,作AB的垂直平分线与AB交于点P即可;
(2)先利用AAS证明△ACP≌△PDB,得出CP=BD=4km,然后在Rt△ACP中利用勾股定理求出AP2=AC2+CP2=32+42=25,则AP=5.
解:(1)连结AB,画出AB的垂直平分线交CD于P,
则点P即为所求的点;
(2)∵∠APB=90°,
∴∠APC+∠BPD=90°,
又∵∠APC+∠CAP=90°,
∴∠CAP=∠BPD,
又∵∠ACP=∠PDB=90°,
∵MN垂直平分AB,
∴AP=BP,
∴△ACP≌△PDB(AAS),
∴CP=BD=4km,
在Rt△ACP中,∠ACP=90°,
AP2=AC2+CP2=32+42=25,
∴AP=5.
答:A村到车站的距离5km.


 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
【题目】计算与化简:
(1)|﹣2|+(﹣2)2﹣(﹣![]() )﹣2﹣(π﹣7)0;
)﹣2﹣(π﹣7)0;
(2)[(﹣x﹣1y﹣2)﹣3﹣y(x2﹣x3y)]÷![]() x2y;
x2y;
(3)![]() ÷(﹣
÷(﹣![]() )3(﹣
)3(﹣![]() )2.
)2.
查看答案和解析>>
科目:初中数学 来源: 题型:
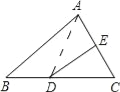
【题目】如图:△ABC的周长为30cm,把△ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D,交AC边与点E,连接AD,若AE=4cm,则△ABD的周长是( )
A. 22cm B. 20cm C. 18cm D. 15cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】台球桌的形状是一个长方形,当母球被击打后可能在不同的边上反弹,为了母球最终击中目标球,击球者需作出不同的设计,确定击球的方向,因此,台球既复杂又有趣,台球运动被称为智慧和技能的较量.

问题1:如图(1),如果母球P击中桌边点A,经桌边反弹击中相邻另一条桌边,再次反弹,那么母球P经过的路线BC与PA平行吗?证明你的判断.
问题2:在一张简易球桌ABCD上,如图(2)所示,目标球F、母球E之间有一个G球阻挡,击球者想通过击打母球E先撞球台的CD边,过一次反弹后再撞击F球,他应将E球打到CD边上的哪一点?
请用尺规作图在图(2)中作出这一点.
问题3:如图(3),在简易球台ABCD上,已知AB=4,BC=3.母球P从角落A以45°角击出,在桌子边缘回弹若干次后,最终必将落入 (填A、B、C、D)角落的球袋,在它落入球袋之前,与桌子边缘共回弹了 次;若AB=100,BC=99,母球P还终将会落入某个角落的球袋,则它在落入球袋之前,在桌子边缘总共回弹了 次.
考点:作图—应用与设计作图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于﹣(﹣a)2的相反数,有下列说法:①等于a2;②等于(﹣a)2;③值可能为0;④值一定是正数.其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=a(x﹣2)2+c,当x=x1时,函数值为y1;当x=x2时,函数值为y2,若|x1﹣2|>|x2﹣2|,则下列表达式正确的是( )
A.y1+y2>0 B.y1﹣y2>0 C.a(y1﹣y2)>0 D.a(y1+y2)>0
查看答案和解析>>
科目:初中数学 来源: 题型:
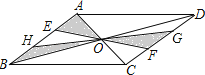
【题目】如图,ABCD的对角线AC、BD相交于点O,EF、GH过点O,且点E、H在边AB上,点G、F在边CD上,向ABCD内部投掷飞镖(每次均落在ABCD内,且落在ABCD内任何一点的机会均等)恰好落在阴影区域的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com