
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 为线段
为线段![]() 的中点,
的中点,![]() 的平分线
的平分线![]() 与
与![]() 轴相较于点
轴相较于点![]() ,
,![]() 、
、![]() 两点关于
两点关于![]() 轴对称.
轴对称.
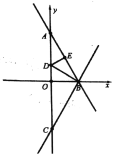

(1)一动点![]() 从点
从点![]() 出发,沿适当的路径运动到直线
出发,沿适当的路径运动到直线![]() 上的点
上的点![]() ,再沿适当的路径运动到点
,再沿适当的路径运动到点![]() 处.当
处.当![]() 的运动路径最短时,求此时点
的运动路径最短时,求此时点![]() 的坐标及点
的坐标及点![]() 所走最短路径的长.
所走最短路径的长.
(2)点![]() 沿直线
沿直线![]() 水平向右运动得点
水平向右运动得点![]() ,平面内是否存在点
,平面内是否存在点![]() 使得以
使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为菱形,若存在,请直接写出点
为顶点的四边形为菱形,若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)点![]() 的坐标为
的坐标为![]() ,点
,点![]() 所走最短路径的长为
所走最短路径的长为![]() ;(2)存在,点
;(2)存在,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)先根据直线的解析式求出点A、B的坐标,再根据直角三角形和角平分线以及对称的性质得出点C、D、E的坐标,然后利用待定系数法可求出直线BC的解析式,最后根据对称性质确定最短路径,求出直线![]() 的解析式,联立两个函数的解析式即可得;
的解析式,联立两个函数的解析式即可得;
(2)根据菱形的性质,分两种情况:BD为边和BD为对角线,然后分别利用菱形的性质、两点之间的距离公式列出等式求解即可.
(1)对于![]()
当![]() 时,
时,![]() ,解得
,解得![]() ,则点B的坐标为
,则点B的坐标为![]()
当![]() 时,
时,![]() ,则点A的坐标为
,则点A的坐标为![]()
![]() 点
点![]() 为线段
为线段![]() 的中点
的中点
![]()
由点A、B的坐标得:![]()
在![]() 中,
中,![]() ,即
,即![]()
![]()
![]() 平分
平分![]()
![]()
在![]() 中,
中,![]() ,即
,即![]()
解得![]()
![]()
![]()
![]()
![]() 、
、![]() 两点关于
两点关于![]() 轴对称
轴对称
![]()
设直线BC的解析式为![]()
将点![]() 代入得
代入得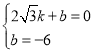 ,解得
,解得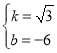
则直线BC的解析式为![]()
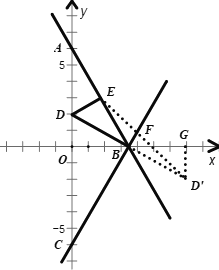
如图,作点D关于直线BC的对称点![]() ,连接ED交BC于点F
,连接ED交BC于点F
由对称的性质、两点之间线段最短可知,点P所走最短路径的长为![]() 的长
的长
由对称的性质可知,![]()
过点![]() 作
作![]() 轴于点G
轴于点G
在![]() 和
和![]() 中,
中,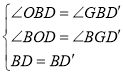
![]()
![]()
![]()
![]()
由两点之间的距离公式得:![]()
设直线![]() 的解析式为
的解析式为![]()
将点![]() 代入得
代入得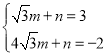 ,解得
,解得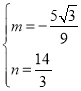
则直线![]() 的解析式为
的解析式为![]()
联立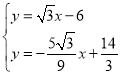 ,解得
,解得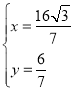
则点![]() 的坐标为
的坐标为![]() ;
;
(2)存在,点![]() 的坐标的求解过程如下:
的坐标的求解过程如下:
![]() ,点
,点![]() 沿直线
沿直线![]() 水平向右运动得点
水平向右运动得点![]()
![]() 可设点
可设点![]() 的坐标为
的坐标为![]() ,且
,且![]()
由菱形的性质,分以下两种情况:
①若BD为边
由菱形的定义得:![]()
由两点之间的距离公式得:![]()
解得![]() 或
或![]() (舍去)
(舍去)
则点![]() 的坐标为
的坐标为![]()
②若BD为对角线
由菱形的定义得:![]()
由两点之间的距离公式得:![]()
解得![]()
则点![]() 的坐标为
的坐标为![]()
综上,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某汽车销售公司一位销售经理1—5月份的汽车销售统计图如下:
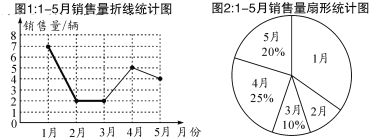
(1)已知1月的销售量是2月的销售量的3.5倍,则1月的销售量为________辆,在扇形图中,2月的销售量所对应的扇形的圆心角大小为________;
(2)补全图中销售量折线统计图;
(3)已知4月份销售的车中有3辆国产车和2辆合资车,国产车分别用G1,G2,G3表示,合资车分别用H1,H2表示,现从这5辆车中随机抽取两辆车参加公司的回馈活动,请用列举法(画树状图或列表)求出“抽到的两辆车都是国产车”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解放碑某商场地下停车场有5个出入口,每天早晨7点开始对外停车且此时车位空置率为80%,在每个出入口的车辆数均是匀速出入的情况下,如果开放2个进口和3个出口,7小时车库恰好停满:如果开放3个进口和2个出口,4小时车库恰好停满.2019年清明节期间,由于商场人数增多,早晨7点时的车位空置率变为60%,又因为车库改造,只能开放2个进口和1个出口,则从早晨7点开始经过_______小时车库恰好停满.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,AD=5,AB=3.若M为射线AD上的一个动点,将△ABM沿BM折叠得到△NBM.若△NBC是直角三角形.则所有符合条件的M点所对应的AM长度的和为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
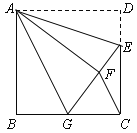
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.
(1)求证:①△ABG≌△AFG; ②BG=GC;
(2)求△FGC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y4x4与x轴,y轴分别交于点A,B,点A在抛物线yax2bx3a(a0)上,将点B向右平移3个单位长度,得到点C.
(1)抛物线的顶点坐标为 (用含a的代数式表示)
(2)若a1,当t-1≤x≤t时,函数yax2bx3a(a0)的最大值为y1,最小值为y2,且y1y22,求t的值;
(3)若抛物线与线段BC恰有一个公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线C1:y=a(x+2)2-5的顶点为P,与x轴相交于A、B两点(点A在点B的左边),点B的横坐标是1.
(1) 求P点坐标及a的值;
(2)如图(1),
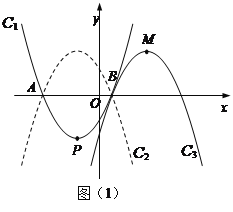
抛物线C2与抛物线C1关于x轴对称,将抛物线C2向右平移,平移后的抛物线记为C3,C3的顶点为M,当点P、M关于点B成中心对称时,求C3的解析式;
(3) 如图(2),
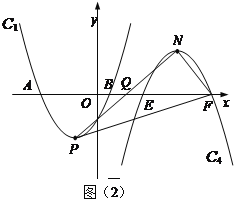
点Q是x轴正半轴上一点,将抛物线C1绕点Q旋转180°后得到抛物线C4.抛物线C4的顶点为N,与x轴相交于E、F两点(点E在点F的左边),当以点P、N、F为顶点的三角形是直角三角形时,求点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com