
����Ŀ����ͼ����֪������C1��y=a(x+2)2-5�Ķ���ΪP����x���ཻ��A��B���㣨��A�ڵ�B����ߣ�����B�ĺ�������1��
(1) ��P�����꼰a��ֵ��
(2)��ͼ��1����
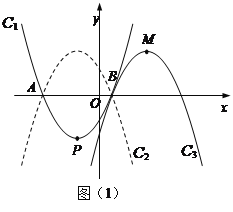
������C2��������C1����x��Գƣ���������C2����ƽ�ƣ�ƽ�ƺ��������ΪC3��C3�Ķ���ΪM������P��M���ڵ�B�����ĶԳ�ʱ����C3�Ľ���ʽ��
(3) ��ͼ��2����
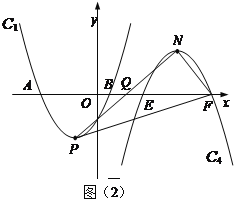
��Q��x����������һ�㣬��������C1�Ƶ�Q��ת180����õ�������C4��������C4�Ķ���ΪN����x���ཻ��E��F���㣨��E�ڵ�F����ߣ������Ե�P��N��FΪ�������������ֱ��������ʱ�����Q�����꣮
���𰸡���1������P��Ϊ��-2��-5����a��![]()
��2��������C3�ı���ʽΪ y=-![]() (x-4)2+5
(x-4)2+5
��3����Q��������![]() ��0����
��0����![]() ��0��ʱ���Ե�P��N��FΪ����
��0��ʱ���Ե�P��N��FΪ����
����������ֱ�������Σ�
��������
(1)��B��1,0������y=a(x+2)2-5�����ɽ��aֵ��
��2������PM����PH��x����H����MG��x����G,����P��M���ڵ�B�����ĶԳƣ�֤����PBH�ա�MBG���������MG��PH��5��BG��BH��3���õ�����M�����꣬�ٸ���������C2��C1����x��ԳƵõ���������C3��C2ƽ�Ƶõ�������д��������C3�ı���ʽ
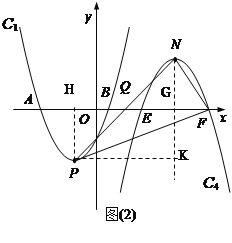
��3������������C4��C1�Ƶ�x���ϵĵ�Q��ת180���õ�����N��������Ϊ5�����N������Ϊ��m,5������PH��x����H����NG��x����G����PK��NG��K�������EF��AB��2BH��6��FG��3����F����Ϊ��m+3��0����H����Ϊ��2��0����K����Ϊ��m��-5����
���ݹ��ɶ�����PN2��NK2+PK2��m2+4m+104��PF2��PH2+HF2��m2+10m+50��NF2��52+32��34���ٷ�����������ۼ���.
(1)��������C1��y=a(x+2)2-5����
����P����-2��-5��
����B��1��0����������C1��
��0= a(1+2)2-5
��ã�a��![]()
(2)����PM����PH��x����H����MG��x����G
����P��M���ڵ�B�����ĶԳ�
��PM����B����PB��MB
���PBH�ա�MBG
��MG��PH��5��BG��BH��3
������M��������4��5��
��������C2��C1����x��ԳƵõ���������C3��C2ƽ�Ƶõ�
��������C3�ı���ʽΪ y=-![]() (x-4)2+5
(x-4)2+5
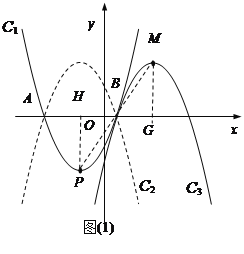
��3����������C4��C1�Ƶ�x���ϵĵ�Q��ת180���õ�
������N��P���ڵ�Q�����ĶԳ�
�ɣ�2���õ�N��������Ϊ5
���N������m��5��
��PH��x����H����NG��x����G����PK��NG��K
����ת����Q��x����
��EF��AB��2BH��6
��FG��3����F������m+3��0����H������2��0����K������m��-5����
PN2��NK2+PK2��m2+4m+104
PF2��PH2+HF2��m2+10m+50
NF2��52+32��34
������PNF��90ʱ��PN2+ NF2��PF2�����m��![]() ��
��
��Q��������![]() ��0��
��0��
������PFN��90ʱ��PF2+ NF2��PN2�����m��![]() ����Q������Ϊ��
����Q��������![]() ��0��
��0��
�ۡ�PN��NK��10��NF�����NPF��90
�������ã���Q������Ϊ��![]() ��0����
��0����![]() ��0��ʱ���Ե�P��N��FΪ����
��0��ʱ���Ե�P��N��FΪ����
����������ֱ�������Σ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣬
���е㣬![]() ��ƽ����
��ƽ����![]() ��
��![]() ������ڵ�
������ڵ�![]() ��
��![]() ��
��![]() �������
�������![]() ��Գƣ�
��Գƣ�
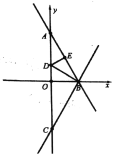

��1��һ����![]() �ӵ�
�ӵ�![]() ���������ʵ���·���˶���ֱ��
���������ʵ���·���˶���ֱ��![]() �ϵĵ�
�ϵĵ�![]() �������ʵ���·���˶�����
�������ʵ���·���˶�����![]() ������
������![]() ���˶�·�����ʱ�����ʱ��
���˶�·�����ʱ�����ʱ��![]() �����꼰��
�����꼰��![]() �������·���ij���
�������·���ij���
��2����![]() ��ֱ��
��ֱ��![]() ˮƽ�����˶��õ�
ˮƽ�����˶��õ�![]() ��ƽ�����Ƿ���ڵ�
��ƽ�����Ƿ���ڵ�![]() ʹ����
ʹ����![]() ��
��![]() ��
��![]() ��
��![]() Ϊ������ı���Ϊ���Σ������ڣ���ֱ��д����
Ϊ������ı���Ϊ���Σ������ڣ���ֱ��д����![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
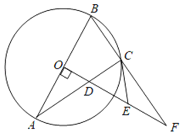
����Ŀ����ͼ����ABC�ڽ��ڡ�O��ABΪֱ������OD��AB��AC�ڵ�D���ӳ�BC��OD���ڵ�F������C����O������CE����OF�ڵ�E��
��1����֤��EC��ED��
��2�����OA��4��EF��3������AC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
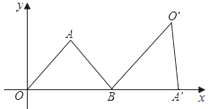
����Ŀ����ͼ����AOBΪ���������Σ�����A�����꣨2��![]() �����ױ�OB��x���ϣ�����AOB�Ƶ�B��˳ʱ�뷽����תһ���ǶȺ����A��O��B����A�Ķ�Ӧ��A����x���ϣ����O��������Ϊ��������
�����ױ�OB��x���ϣ�����AOB�Ƶ�B��˳ʱ�뷽����תһ���ǶȺ����A��O��B����A�Ķ�Ӧ��A����x���ϣ����O��������Ϊ��������
A. ��![]() ��
��![]() �� B. ��
�� B. ��![]() ��
��![]() �� C. ��
�� C. ��![]() ��
��![]() �� D. ��
�� D. ��![]() ��4
��4![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У����κ���y=x2+2x��3��ͼ����ͼ��ʾ����A��x1��y1����B��x2��y2���Ǹö��κ���ͼ���ϵ����㣬���Щ�3��x1��x2��0�������н�����ȷ���ǣ�������
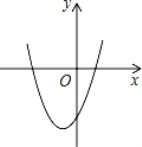
A. y1��y2B��y1��y2C��y����Сֵ�ǩ�3 D��y����Сֵ�ǩ�4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�����![]() (
(![]() )��ͼ���߳�Ϊ2��������OABC�Ķ���B����ͼ��ֱ��
)��ͼ���߳�Ϊ2��������OABC�Ķ���B����ͼ��ֱ��![]() ��
��![]() (
(![]() )��ͼ���ڵ�D(��D��ֱ��BC���Ϸ�)����x�ύ�ڵ�E .
)��ͼ���ڵ�D(��D��ֱ��BC���Ϸ�)����x�ύ�ڵ�E .
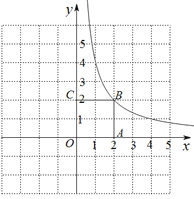
(1)��k��ֵ��
(2)�ᡢ�����궼�������ĵ��������.��![]() (
(![]() )��ͼ���ڵ�B��D֮��IJ������߶�AB��AE��DEΧ�ɵ�����(�����߽�)ΪW.
)��ͼ���ڵ�B��D֮��IJ������߶�AB��AE��DEΧ�ɵ�����(�����߽�)ΪW.
�ٵ�![]() ʱ��ֱ��д������W�ڵ����������
ʱ��ֱ��д������W�ڵ����������
��������W��ǡ��3�����㣬��Ϻ���ͼ����m��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�BC��AB��AC���ס�����������BC��ȡһ��P��ʹ�á�APC��2��ABC�����������£�
���ף���AB���д��ߣ���BC��P�㣬��P��Ϊ����
���ң���BΪԲ�ģ�AB��Ϊ�뾶��������BC��P�㣬��P��Ϊ����
�������˵������������жϺ�����ȷ����������
![]()
A. ���˽���ȷB. ���˽Դ���C. ����ȷ���Ҵ���D. �״�������ȷ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���֪AB��BC��CA��4cm��AD��BC��D����P��Q�ֱ��BC����ͬʱ���������е�P��BC���յ�C�˶����ٶ�Ϊ1cm/s����Q��CA��AB���յ�B�˶����ٶ�Ϊ2cm/s���������˶���ʱ��Ϊx��s����
��1����xΪ��ֵʱ��PQ��AC��
��2�����PQD�����Ϊy��cm2������0��x��2ʱ����y��x�ĺ�����ϵʽ��
��3��̽����PQΪֱ����Բ��AC��λ�ù�ϵ����д����Ӧλ�ù�ϵ��x��ȡֵ��Χ��
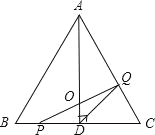
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ACB��90�㣬�ֱ��Ե�A��CΪԲ�ģ��Դ���![]() AC�ij�Ϊ�뾶�����������ཻ�ڵ�D��E����ֱ��DE��AB�ڵ�F����AC�ڵ�G������CF���Ե�CΪԲ�ģ���CF�ij�Ϊ�뾶��������AC�ڵ�H������A��30�㣬BC��2����AH�ij���(����)
AC�ij�Ϊ�뾶�����������ཻ�ڵ�D��E����ֱ��DE��AB�ڵ�F����AC�ڵ�G������CF���Ե�CΪԲ�ģ���CF�ij�Ϊ�뾶��������AC�ڵ�H������A��30�㣬BC��2����AH�ij���(����)
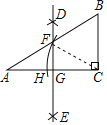
A. ![]() B. 2C.
B. 2C. ![]() +1D. 2
+1D. 2![]() ��2
��2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com