
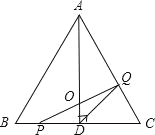
【题目】如图,在△ABC中,已知AB=BC=CA=4cm,AD⊥BC于D,点P,Q分别从BC两点同时出发,其中点P沿BC向终点C运动.速度为1cm/s;点Q沿CA、AB向终点B运动,速度为2cm/s,设它们运动的时间为x(s).
(1)求x为何值时,PQ⊥AC;
(2)设△PQD的面积为y(cm2),当0<x<2时,求y与x的函数关系式;
(3)探索以PQ为直径的圆与AC的位置关系,请写出相应位置关系的x的取值范围.
【答案】(1)x=![]() ;(2)y
;(2)y![]() ;(3)当x=
;(3)当x=![]() 或
或![]() 时,以PQ为直径的圆与AC相切,当0≤x<
时,以PQ为直径的圆与AC相切,当0≤x<![]() 或
或![]() <x<
<x<![]() 或
或![]() <x≤4时,以PQ为直径的圆与AC相交.
<x≤4时,以PQ为直径的圆与AC相交.
【解析】
(1)若使PQ⊥AC,则当Q在AC上,根据路程=速度×时间表示出CP和CQ的长,再根据含30度的直角三角形的性质列方程求解;
(2)过点Q作QN⊥BC于N,利用三角函数求出QN,然后表示出DP,再根据三角形面积公式进行求解;
(3)可分点Q在AC和AB上两种情况讨论:当Q在AC时,根据(1)即可解决问题;当Q在AB上时,设以PQ为直径的圆与AC相切于点G,连接O′G,易证PQ=2O′G=QE+PF=![]() ,过点Q作QN⊥BC于N,在Rt△BNQ中,运用三角函数可得QN=
,过点Q作QN⊥BC于N,在Rt△BNQ中,运用三角函数可得QN=![]() ,BN=4x,则有PN=2x4,然后在Rt△QNP中,运用勾股定理即可解决问题.
,BN=4x,则有PN=2x4,然后在Rt△QNP中,运用勾股定理即可解决问题.
解:(1)当Q在AB上时,显然PQ不垂直于AC,
当Q在AC上时,由题意得,BP=x,CQ=2x,则PC=4x,
∵AB=BC=CA=4,
∴∠C=60°,
若PQ⊥AC,则有∠QPC=30°,
∴PC=2CQ,即4x=2×2x,
∴x=![]() ,
,
即当x=![]() 时,PQ⊥AC;
时,PQ⊥AC;
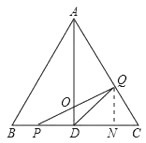
(2)如图,当0<x<2时,P在BD上,Q在AC上,过点Q作QN⊥BC于N,
∵∠C=60°,QC=2x,
∴QN=QC·sin60°=![]() ,
,
∵AB=AC,AD⊥BC,
∴BD=CD=![]() BC=2,
BC=2,
∴DP=2x,/span>
∴y=![]() PDQN=
PDQN=![]() ;
;
(3)显然,不存在x的值,使得以PQ为直径的圆与AC相离,
①当点Q在AC上时,由(1)可知,当x=![]() 时,以PQ为直径的圆与AC相切;
时,以PQ为直径的圆与AC相切;
②当点Q在AB时,如图,
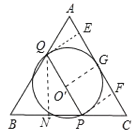
设以PQ为直径的圆与AC相切于点G,圆心为O′,连接O′G,则有O′G⊥AC,
过点Q作QE⊥AC于E,过点P作PF⊥AC于F,则QE∥O′G∥PF,
∵QO′=PO′,
∴EG=FG,
∴O′G=![]() (QE+PF),
(QE+PF),
∴PQ=2O′G=QE+PF,
由题意可得,CP=4x,AQ=2x4,
∴QE=AQsin60°=![]() ,PF=PCsin60°=
,PF=PCsin60°=![]() ,
,
∴PQ=![]() ,
,
过点Q作QN⊥BC于N,
在Rt△BNQ中,QN=BQsin60°=![]() ,BN=BQcos60°=
,BN=BQcos60°=![]() (82x)=4x,
(82x)=4x,
∴PN=x(4x)=2x4,
在Rt△QNP中,根据勾股定理可得: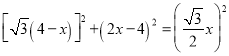 ,
,
整理可得:25x2160x+256=0,
解得:x1=x2=![]() ,
,
综上所述,当x=![]() 或
或![]() 时,以PQ为直径的圆与AC相切,当0≤x<
时,以PQ为直径的圆与AC相切,当0≤x<![]() 或
或![]() <x<
<x<![]() 或
或![]() <x≤4时,以PQ为直径的圆与AC相交.
<x≤4时,以PQ为直径的圆与AC相交.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y4x4与x轴,y轴分别交于点A,B,点A在抛物线yax2bx3a(a0)上,将点B向右平移3个单位长度,得到点C.
(1)抛物线的顶点坐标为 (用含a的代数式表示)
(2)若a1,当t-1≤x≤t时,函数yax2bx3a(a0)的最大值为y1,最小值为y2,且y1y22,求t的值;
(3)若抛物线与线段BC恰有一个公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线C1:y=a(x+2)2-5的顶点为P,与x轴相交于A、B两点(点A在点B的左边),点B的横坐标是1.
(1) 求P点坐标及a的值;
(2)如图(1),
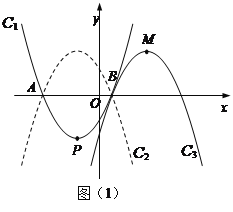
抛物线C2与抛物线C1关于x轴对称,将抛物线C2向右平移,平移后的抛物线记为C3,C3的顶点为M,当点P、M关于点B成中心对称时,求C3的解析式;
(3) 如图(2),
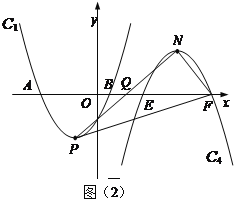
点Q是x轴正半轴上一点,将抛物线C1绕点Q旋转180°后得到抛物线C4.抛物线C4的顶点为N,与x轴相交于E、F两点(点E在点F的左边),当以点P、N、F为顶点的三角形是直角三角形时,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
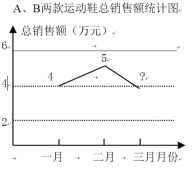
【题目】某运动品牌对第一季度A、B两款运动鞋的销售情况进行统计,两款运动鞋的销售量及总销售额如图所示:
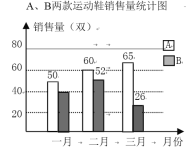
(1)一月份B款运动鞋的销售量是A款的80%,则一月份B款运动鞋销售了多少双?
(2)第一季度这两款运动鞋的销售单价保持不变,求三月份的总销售额(销售额=销售单价×销售量)
(3)结合第一季度的销售情况,请你对这两款运动鞋的进货、销售等方面提出一条建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
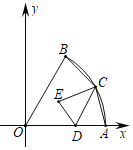
【题目】如图,扇形OAB中,∠AOB=60°,OA=4,点C为弧AB的中点,D为半径OA上一点,点A关于直线CD的对称点为E,若点E落在半径OA上,则OE=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
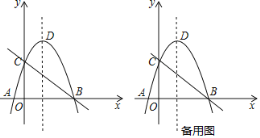
【题目】如图,直线y=﹣x+3与x轴、y轴分别交于B、C两点,抛物线y=﹣x2+bx+c经过B、C两点,与x轴另一交点为A,顶点为D.
(1)求抛物线的解析式;
(2)在x轴上找一点E,使△EDC的周长最小,求符合条件的E点坐标;
(3)在抛物线的对称轴上是否存在一点P,使得∠APB=∠OCB?若存在,求出PB2的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
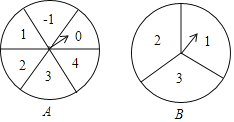
【题目】如图,转盘A中的6个扇形的面积相等,转盘B中的3个扇形的面积相等.分别任意转动转盘A、B各1次,当转盘停止转动时,将指针所落扇形中的2个数字分别作为平面直角坐标系中一个点的横坐标、纵坐标.
(1)用表格列出这样的点所有可能的坐标;
(2)求这些点落在二次函数y=x2﹣5x+6的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
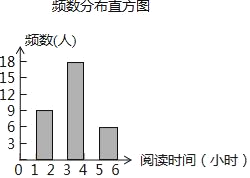
【题目】向阳中学为了解全校学生利用课外时间阅读的情况,调查者随机抽取若干名学生,调查他们一周的课外阅读时间,并根据调查结果绘制了如下尚不完整的统计表(图).根据图表信息,解答下列问题:
频率分布表
阅读时间(小时) | 频数(人) | 频率 |
1≤x<2 | 9 | 0.15 |
2≤x<3 | a | m |
3≤x<4 | 18 | 0.3 |
4≤x<5 | 12 | n |
5≤x<6 | 6 | 0.1 |
合计 | b | 1 |
(1)填空:a= ,b= ,m= ,n= ;
(2)将频数分布直方图补充完整;
(3)阅读时间不低于5小时的6人中,有2名男生、4名女生.现从这6名学生中选取两名同学进行读书宣讲,求选取的两名学生恰好是两名女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com