
����Ŀ����ű�ij�̳�����ͣ������5������ڣ�ÿ���糿7�㿪ʼ����ͣ���Ҵ�ʱ��λ������Ϊ80%����ÿ������ڵij������������ٳ��������£��������2�����ں�3�����ڣ�7Сʱ����ǡ��ͣ�����������3�����ں�2�����ڣ�4Сʱ����ǡ��ͣ����2019���������ڼ䣬�����̳��������࣬�糿7��ʱ�ij�λ�����ʱ�Ϊ60%������Ϊ������죬ֻ�ܿ���2�����ں�1�����ڣ�����糿7�㿪ʼ����_______Сʱ����ǡ��ͣ����
���𰸡�![]()
��������
����1������1Сʱ����![]() ������1������1Сʱ����
������1������1Сʱ����![]() ��������λ������
�������������![]()
������֪�����������2�����ں�3�����ڣ�7Сʱ����ǡ��ͣ�������г�����![]()
������֪�����������3�����ں�2�����ڣ�4Сʱ����ǡ��ͣ�������г�����![]()
����������![]() ��
��![]() ����
����![]() �Ĺ�ϵʽ
�Ĺ�ϵʽ
������������ʱ�Ϊ60%��ֻ�ܿ���2�����ں�1������ʱ������Сʱͣ����![]() ��
��![]() ��
��![]() ����
����![]() �Ĺ�ϵʽ���뼴�����.
�Ĺ�ϵʽ���뼴�����.
��1������1Сʱ����![]() ������1������1Сʱ����
������1������1Сʱ����![]() ��������λ������
�������������![]()
![]()
��ã�
![]() ��Сʱ��
��Сʱ��
�ʴ�Ϊ��![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
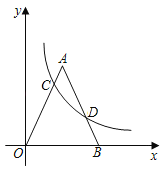
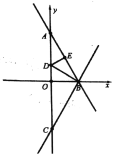
����Ŀ����ͼ��ʾ����ֱ������ϵ�У�OΪԭ�㣬������A0B�Ķ���B��x������AO��AB��A��������(![]() ��5)������������y��
��5)������������y��![]() ��ͼ����AO���ڵ�C����AB���ڵ�D����OC��2BD����k��ֵ��_____��
��ͼ����AO���ڵ�C����AB���ڵ�D����OC��2BD����k��ֵ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
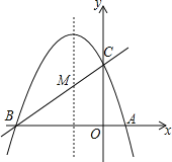
����Ŀ����ͼ����֪������y=ax2+bx+c��a��0���ĶԳ���Ϊֱ��x=-1���������߾���A��1��0����C��0��3�����㣬��x�ύ�ڵ�B��
��1����ֱ��y=mx+n����B��C���㣬��ֱ��BC�������ߵĽ���ʽ��
��2���������ߵĶԳ���x=-1����һ��M��ʹ��M����A�ľ����뵽��C�ľ���֮����С�������M�����ꣻ
��3�����PΪ�����ߵĶԳ���x=-1�ϵ�һ�����㣬��ʹ��BPCΪֱ�������εĵ�P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
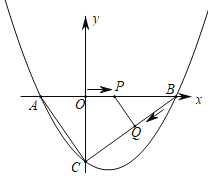
����Ŀ����ͼ����������x�ύ��A��B����(��A�ڵ�B���)����y�ύ�ڵ�C���ҵ�x����1��x��3ʱ��yֵ��ȣ�ֱ��y��![]() �����������������㣬����һ������ĺ�������6����һ�����������������ߵĶ���M��
�����������������㣬����һ������ĺ�������6����һ�����������������ߵĶ���M��
(1)�����������ߵı���ʽ��
(2)����P��ԭ��O���������߶�OB����ÿ��1����λ���ȵ��ٶ����B�˶���ͬʱ��Q�ӵ�B���������߶�BC����ÿ��2����λ���ȵ��ٶ����C�˶�����һ���㵽���յ�ʱ����һ��������ֹͣ�˶������˶�ʱ��Ϊt�룮
����t��ȡֵ��Χ��
����ʹ��BPQΪֱ�������Σ����������������tֵ��
��tΪ��ֵʱ���ı���ACQP���������Сֵ����Сֵ�Ƕ��٣�ֱ��д���𰸣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
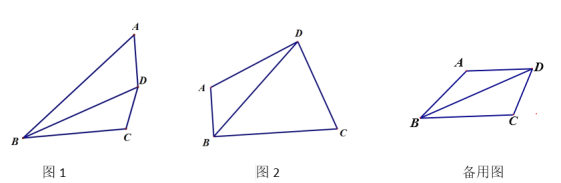
����Ŀ�����ı��� ABCD �У�BD ƽ�֡�ABC��
��1����ͼ 1������BAD=��BDC����֤��BD2=ABBC��
��2����ͼ 2����A>90������BAD+��BDC=180����
������ABC=90�㣬AB=![]() ��BC=8����BD�ij���
��BC=8����BD�ij���
���� BC=3CD=3a��BD=9�� �� AB �ij�Ϊ �� (�ú� a �Ĵ���ʽ��ʾ)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ��һ������1��������������![]() ����1����
����1����![]() ����1����
����1����![]() ����1��������3����1����2����1����ô�����������Ϊ����
����1��������3����1����2����1����ô�����������Ϊ����![]() ������
������![]() ȡ������磺73����5����3����4����1����3����1����2����1����ô73Ϊ������������
ȡ������磺73����5����3����4����1����3����1����2����1����ô73Ϊ������������
���϶�����![]() ��������3��2����С������Ϊ
��������3��2����С������Ϊ![]() ����ô����
����ô����![]() �������Ա�ʾΪ
�������Ա�ʾΪ![]() ��
��![]() Ϊ�������������磺6��5��4��3��2����С������Ϊ60����ô�������������Ա�ʾΪ
Ϊ�������������磺6��5��4��3��2����С������Ϊ60����ô�������������Ա�ʾΪ![]() ��
��![]() ��������
��������
��1�������С����λ������������
��2��һ�������������롰���������ĺ�Ϊ170���������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ij�ֶ�ͯ��ߣ����ÿ������Ϊ40Ԫ���г��������Ź涨���������ÿ�������ܳ���60Ԫ����ÿ����۳�50���������г����鷢�֣����۵���ÿ����2Ԫ��ÿ�������������1���������۵�������![]() Ԫ��ÿ���۳�
Ԫ��ÿ���۳�![]() ����
����
��1�����![]() ��
��![]() ֮��ĺ�������ʽ��
֮��ĺ�������ʽ��
��2����![]() Ϊ����ʱ������ÿ������������߿ɻ�����2250Ԫ��
Ϊ����ʱ������ÿ������������߿ɻ�����2250Ԫ��
��3���賬��ÿ������������߿ɻ���![]() Ԫ����
Ԫ����![]() Ϊ����ʱ
Ϊ����ʱ![]() ������ֵ�Ƕ��٣�
������ֵ�Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣬
���е㣬![]() ��ƽ����
��ƽ����![]() ��
��![]() ������ڵ�
������ڵ�![]() ��
��![]() ��
��![]() �������
�������![]() ��Գƣ�
��Գƣ�

��1��һ����![]() �ӵ�
�ӵ�![]() ���������ʵ���·���˶���ֱ��
���������ʵ���·���˶���ֱ��![]() �ϵĵ�
�ϵĵ�![]() �������ʵ���·���˶�����
�������ʵ���·���˶�����![]() ������
������![]() ���˶�·�����ʱ�����ʱ��
���˶�·�����ʱ�����ʱ��![]() �����꼰��
�����꼰��![]() �������·���ij���
�������·���ij���
��2����![]() ��ֱ��
��ֱ��![]() ˮƽ�����˶��õ�
ˮƽ�����˶��õ�![]() ��ƽ�����Ƿ���ڵ�
��ƽ�����Ƿ���ڵ�![]() ʹ����
ʹ����![]() ��
��![]() ��
��![]() ��
��![]() Ϊ������ı���Ϊ���Σ������ڣ���ֱ��д����
Ϊ������ı���Ϊ���Σ������ڣ���ֱ��д����![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
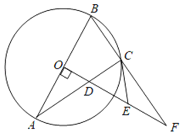
����Ŀ����ͼ����ABC�ڽ��ڡ�O��ABΪֱ������OD��AB��AC�ڵ�D���ӳ�BC��OD���ڵ�F������C����O������CE����OF�ڵ�E��
��1����֤��EC��ED��
��2�����OA��4��EF��3������AC�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com