
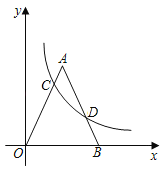
【题目】如图所示,在直角坐标系中,O为原点,等腰△A0B的顶点B在x轴土,AO=AB,A点坐标是(![]() ,5),反比例函数y=
,5),反比例函数y=![]() 的图象与AO交于点C,与AB交于点D,且OC=2BD,则k的值是_____.
的图象与AO交于点C,与AB交于点D,且OC=2BD,则k的值是_____.
【答案】8
【解析】
作AE⊥OB于E,CM⊥OB于M,DN⊥OB于N,首先证得△COM∽△DBN,得出CM=2DN,OM=2BN,设D(![]() ,n),C(
,n),C(![]() ,2n),进一步得出
,2n),进一步得出![]() =2(5﹣
=2(5﹣![]() )①,通过证得△COM∽△AOE,根据相似三角形的性质得出CM=2OM,进一步得出k=2n2②,把②代入①得,n=10﹣4n,解得n=2,即可求得k的值.
)①,通过证得△COM∽△AOE,根据相似三角形的性质得出CM=2OM,进一步得出k=2n2②,把②代入①得,n=10﹣4n,解得n=2,即可求得k的值.
解:作AE⊥OB于E,CM⊥OB于M,DN⊥OB于N,
∵OA=OB,
∴∠AOB=∠ABO,
∵∠CMO=∠DNB=90°,
∴△COM∽△DBN,
∴![]() =
=![]() =
=![]()
∵OC=2BD,
∴CM=2DN,OM=2BN,
设DN=n,则D(![]() ,n),C(
,n),C(![]() ,2n),
,2n),
∵AO=AB,A点坐标是(![]() ,5),
,5),
∴OE=BE=![]() ,OB=5,AE=5,
,OB=5,AE=5,
∴AE=2OE,BN=5﹣![]() ,
,
∴![]() =2(5﹣
=2(5﹣![]() )①,
)①,
∵CM∥AE,
∴△COM∽△AOE,
∴![]() =
=![]() =2,
=2,
∴CM=2OM,
∴2n=2×![]() ,
,
∴k=2n2②
把②代入①得,n=10﹣4n,
解得n=2,
∴k=2×22=8,
故答案为8.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】每到春夏交替时节,雌性杨树会以满天飞絮的方式来传播下一代,漫天飞舞的杨絮易引发皮肤病、呼吸道疾病等,给人们造成困扰,为了解市民对治理杨絮方法的赞同情况,某课题小组随机调查了部分市民(问卷调查表如表所示),并根据调查结果绘制了如下尚不完整的统计图.
治理杨絮一一您选哪一项?(单选)
A.减少杨树新增面积,控制杨树每年的栽种量
B.调整树种结构,逐渐更换现有杨树
C.选育无絮杨品种,并推广种植
D.对雌性杨树注射生物干扰素,避免产生飞絮
E.其他
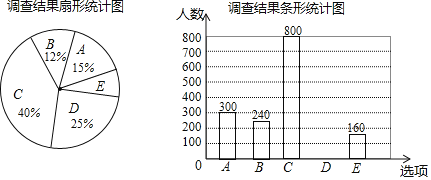
根据以上统计图,解答下列问题:
(1)本次接受调查的市民共有 人;
(2)扇形统计图中,扇形E的圆心角度数是 ;
(3)请补全条形统计图;
(4)若该市约有90万人,请估计赞同“选育无絮杨品种,并推广种植”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,![]() 为矩形
为矩形![]() 的边
的边![]() 上一点,动点
上一点,动点![]() 同时从点
同时从点![]() 出发,点
出发,点![]() 沿折线
沿折线![]() 运动到点
运动到点![]() 时停止,点
时停止,点![]() 沿
沿![]() 运动到点
运动到点![]() 时停止,它们运动的速度都是
时停止,它们运动的速度都是![]() 秒.设
秒.设![]() 同时出发
同时出发![]() 秒时,
秒时,![]() 的面积为
的面积为![]() ,已知
,已知![]() 与
与![]() 的函数关系图象如图2所示.请回答:
的函数关系图象如图2所示.请回答:
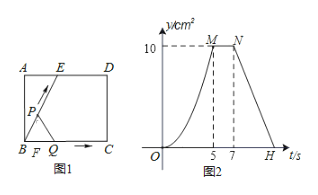
(1)线段![]() 的长为_______cm;
的长为_______cm;
(2)当运动时间![]() 秒时,
秒时,![]() 之间的距离是_______
之间的距离是_______![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的二次函数y=ax2-(2a+2)x+b(a≠0)在x=0和x=6时函数值相等.
(1)求a的值;
(2)若该二次函数的图象与直线y=-2x的一个交点为(2,m),求它的解析式;
(3)在(2)的条件下,直线y=-2x-4与x轴,y轴分别交于A,B,将线段AB向右平移n(n>0)个单位,同时将该二次函数在2≤x≤7的部分向左平移n个单位后得到的图象记为G,请结合图象直接回答,当图象G与平移后的线段有公共点时,n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
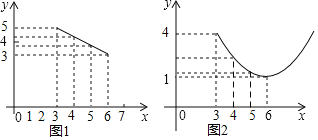
【题目】某种蔬菜每千克售价y1(元)与销售月份x之间的关系如图1所示,每千克成本y2(元)与销售月份x之间的关系如图2所示,其中图1中的点在同一条线段上,图2中的点在对称轴平行于y轴的同一条抛物线上,且抛物线的最低点的坐标为(6,1).
(1)求出y1与x函数关系式;
(2)求出y2与x函数关系式;
(3)设这种蔬菜每千克收益为w元,试问在哪个月份出售这种蔬菜,w将取得最大值?并求出此最大值.(收益=售价﹣成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,二次函数![]() (
(![]() ,
,![]() ,
,![]() 是常数,
是常数,![]() )的图象的一部分与
)的图象的一部分与![]() 轴的交点
轴的交点![]() 在
在![]() 与
与![]() 之间,对称轴为直线
之间,对称轴为直线![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() (
(![]() 为实数);⑤当
为实数);⑤当![]() 时,
时,![]() .其中,正确结论的个数是( )
.其中,正确结论的个数是( )
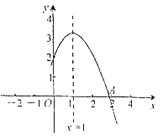
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车销售公司一位销售经理1—5月份的汽车销售统计图如下:
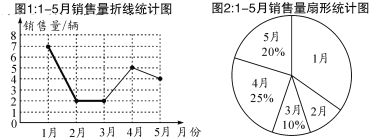
(1)已知1月的销售量是2月的销售量的3.5倍,则1月的销售量为________辆,在扇形图中,2月的销售量所对应的扇形的圆心角大小为________;
(2)补全图中销售量折线统计图;
(3)已知4月份销售的车中有3辆国产车和2辆合资车,国产车分别用G1,G2,G3表示,合资车分别用H1,H2表示,现从这5辆车中随机抽取两辆车参加公司的回馈活动,请用列举法(画树状图或列表)求出“抽到的两辆车都是国产车”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解放碑某商场地下停车场有5个出入口,每天早晨7点开始对外停车且此时车位空置率为80%,在每个出入口的车辆数均是匀速出入的情况下,如果开放2个进口和3个出口,7小时车库恰好停满:如果开放3个进口和2个出口,4小时车库恰好停满.2019年清明节期间,由于商场人数增多,早晨7点时的车位空置率变为60%,又因为车库改造,只能开放2个进口和1个出口,则从早晨7点开始经过_______小时车库恰好停满.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com