
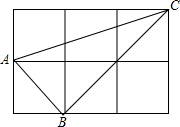
 如图,小正方形的边长为1.联结小正方形的三个顶点,得△ABC,求图中△ABC的边AC上的高.
如图,小正方形的边长为1.联结小正方形的三个顶点,得△ABC,求图中△ABC的边AC上的高. 分析 由小正方形的边长为1,根据勾股定理得到AB=$\sqrt{2}$,BC=2$\sqrt{2}$,AC=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,由于AB2+BC2=AC2,根据勾股定理的逆定理得到∠B=90°,然后根据三角形的面积列方程即可得到结论.
解答 解:∵小正方形的边长为1,
∴AB=$\sqrt{2}$,BC=2$\sqrt{2}$,AC=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
∴AB2+BC2=AC2,
∴∠B=90°,
设AC上的高为h,
∴S△ABC=$\frac{1}{2}•AB•BC$=$\frac{1}{2}$AC•h,
∴h=$\frac{2\sqrt{10}}{5}$,
∴△ABC的边AC上的高为$\frac{2\sqrt{10}}{5}$.
点评 本题考查了勾股定理,勾股定理的逆定理,正方形的性质,熟练掌握勾股定理是解题的关键.


科目:初中数学 来源: 题型:填空题
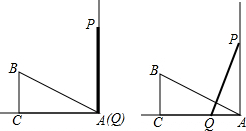 已知墙面与地面成直角,直角△ABC如图放置,BC=3cm,AC=4cm,AB=5cm,一木棒PQ靠在墙上,且PQ=5cm.木棒沿墙面滑下(P向A运动,Q向C运动),P点运动到A点就停止运动,已知P点的运动速度是1cm/s,当P运动1或2s时,△ABC与△PQA全等.
已知墙面与地面成直角,直角△ABC如图放置,BC=3cm,AC=4cm,AB=5cm,一木棒PQ靠在墙上,且PQ=5cm.木棒沿墙面滑下(P向A运动,Q向C运动),P点运动到A点就停止运动,已知P点的运动速度是1cm/s,当P运动1或2s时,△ABC与△PQA全等.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com