
【题目】如图,四边形ABCD是平行四边形,以AB为直径的圆O经过点D,E是⊙O上一点,且∠AED=45°. 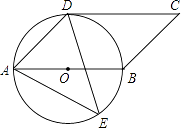
(1)判断CD与⊙O的位置关系,并说明理由;
(2)若⊙O半径为6cm,AE=10cm,求∠ADE的正弦值.
【答案】
(1)解:CD与⊙O相切.
理由:连接OD,
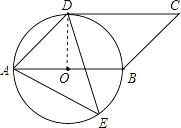
∵∠AED=45°,
∴∠AOD=2∠AED=90°,
即OD⊥AB,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴OD⊥CD,
∵AB为直径的圆O经过点D,
∴CD与⊙O相切;
(2)解:过点O作OF⊥AE,连接OE,
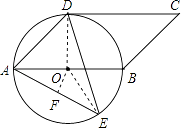
则AF= ![]() AE=
AE= ![]() ×10=5(cm),
×10=5(cm),
∵OA=OE,
∴∠AOF= ![]() ∠AOE,
∠AOE,
∵∠ADE= ![]() ∠AOE,
∠AOE,
∴∠ADE=∠AOF,
在Rt△AOF中,sin∠AOF= ![]() =
= ![]() ,
,
∴sin∠ADE= ![]() .
.
【解析】(1)首先连接OD,由在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半,即可证得OD⊥AB,又由四边形ABCD是平行四边形,即可证得OD⊥CD,即可证得CD与⊙O相切;(2)首先过点O作OF⊥AE,连接OE,由垂径定理可得AF=5cm,∠AOF= ![]() ∠AOE,又由圆周角定理可得∠ADE=
∠AOE,又由圆周角定理可得∠ADE= ![]() ∠AOE,继而证得∠AOF=∠ADE,然后在Rt△AOF中,求得sin∠AOF的值,即可求得答案.
∠AOE,继而证得∠AOF=∠ADE,然后在Rt△AOF中,求得sin∠AOF的值,即可求得答案.
【考点精析】本题主要考查了平行四边形的性质和切线的判定定理的相关知识点,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,点A在双曲线y= ![]() 上,点B在双曲线y=
上,点B在双曲线y= ![]() (k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )
(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )
A.6
B.9
C.10
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△OAB的顶点A(﹣2,4)在抛物线y=ax2上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为( )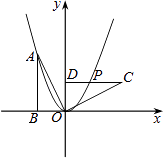
A.( ![]() ,
, ![]() )
)
B.(2,2)
C.( ![]() ,2)
,2)
D.(2, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,△ABC顶点的横、纵坐标都是整数.若将△ABC以某点为旋转中心,顺时针旋转90°得到△DEF,则旋转中心的坐标是( )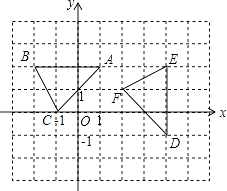
A.(0,0)
B.(1,0)
C.(1,﹣1)
D.(2.5,0.5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线相交于坐标原点,点A的坐标为(a,2),点B的坐标为(﹣1,﹣ ![]() ),点C的坐标为(2
),点C的坐标为(2 ![]() ,c),那么a,c的值分别是( )
,c),那么a,c的值分别是( ) 
A.a=﹣1,c=﹣ ![]()
B.a=﹣2 ![]() ,c=﹣2
,c=﹣2
C.a=1,c= ![]()
D.a=2 ![]() ,c=2
,c=2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知A(1,2),B(3,1),C(﹣2,﹣1).
(1)在图中作出△ABC关于y轴对称的△A1B1C1.
(2)直接写出点A1,B1,C1的坐标.
A1 , B1 , C1 ;
(3)请你求出△A1B1C1的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,AB是⊙O的直径,C为⊙O上一点,AD垂直于经过点C的直线DE,垂足为点D,AC平分∠DAB.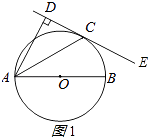
(1)求证:直线DE是⊙O的切线;
(2)连接BC,猜想:∠ECB与∠CAB的数量关系,并证明你的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com