练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
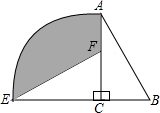
    如图，在平面内将Rt△ABC绕着直角顶点C逆时针旋转90°，得到Rt△EFC，若AB=
    		5
    ，BC=1，则阴影部分的面积为
     
    ．
    考点：扇形面积的计算,旋转的性质
    专题：
    分析：先根据勾股定理求出AC的长，由图形旋转的性质得出AC=EC，BC=FC，再根据S阴影=S扇形-S△ECF即可得出结论．
    解答：解：∵Rt△ABC中AB=
    		5
    ，BC=1，
    ∴AC=
    		AB2-BC2
    =
    		(
    		5
    )    2    -12
    =2．
    ∵△EFC由△ABC旋转而成，
    ∴△EFC≌△ABC，
    ∴AC=EC=2，BC=FC=1，
    ∴S阴影=S扇形-S△ECF=
    90π×22
    360
    -
    1
    2
    ×2×1=π-1．
    故答案为：π-1．
    点评：本题考查的是扇形面积的计算，熟记扇形的面积公式是解答此题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，已知△ABC是等边三角形，D为AC边上的一点，DG∥AB，延长AB到E，使BE=GD，连接DE交BC于F．
    （1）求证：GF=BF；
    （2）若△ABC的边长为a，BE的长为b，且a，b满足（a-7）2+b2-6b+9=0，求BF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    下列图形是正方体侧面展开图的是（　　）
    A、
    B、
    C、
    D、

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，它可以看作“”通过连续平移
     
    次得到的，看作“”绕中心旋转
     
    次，每次旋转
     
    度得到的．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

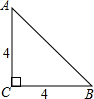    已知如图，是腰长为4的等腰直角三角形ABC，要求在其内部作出一个半圆，直径在△ABC的边上，且半圆的弧与△ABC的其他两边相切，则该半圆的半径是
     
    （结果保留根号）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

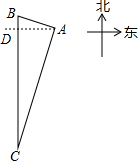    如图，某国3艘炮艇正追袭5条中国渔船，“中国渔政310”船（用“A”表示）接到陆地指挥中心（用“B”表示）命令疾速驰救中国渔船，渔船（用“C”表示）位于陆地指挥中心正南方向．经测定AB=
    		6
    海里，BC=
    		24
    海里，C=
    		18
    海里，∠BAC=90°，求A到BC的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在△ABC中，
    AG
    DE
    =
    AH
    BC
    ，且DE=24，BC=30，GH=8，求AH的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    概念理解
    把一个或几个图形分割后，不重叠、无缝隙的重新拼成另一个图形的过程叫做“剖分-重拼”．如图①，一个有一组对边平形的四边形可以剖分-重拼为一个三角形；如图②，任意两个正方形可以剖分-重拼为一个正方形．
    尝试操作
    （1）如图③，把图中的三角形剖分-重拼为一个矩形（只要画出示意图，不需说明操作步骤）；
    阅读解释
    （2）如何把一个矩形ABCD（如图④）剖分-重拼为一个正方形呢？操作如下：
    Ⅰ．画辅助图．作射线OX，在射线OX上截取OM=AB，MN=BC．以ON为直径作半圆，过点M作MI⊥射线OX，与半圆交于点I；
    Ⅱ．图④中，在CD上取点F，使AF=MI，作BE⊥AF，垂足为E．把△ADF沿射线DC平移到△BCH的位置，把△AEB沿射线AF平移到△FGH的位置，得四边形EBHG．
    请说明按照上述操作方法得到的四边形EBHG是正方形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    计算：
    ①1.5°=
     
    ′=
     
    ″；
    ②450″=
     
    ′=
     
    °；
    ③90°-54°48′6″=
     
    ．

    查看答案和解析>>

    同步练习册答案