
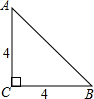
 已知如图,是腰长为4的等腰直角三角形ABC,要求在其内部作出一个半圆,直径在△ABC的边上,且半圆的弧与△ABC的其他两边相切,则该半圆的半径是
已知如图,是腰长为4的等腰直角三角形ABC,要求在其内部作出一个半圆,直径在△ABC的边上,且半圆的弧与△ABC的其他两边相切,则该半圆的半径是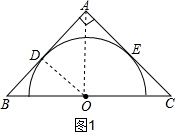
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
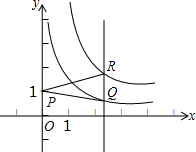 函数y=
函数y=| 1 |
| x |
| 4 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
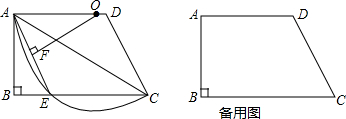
查看答案和解析>>
科目:初中数学 来源: 题型:
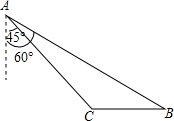 如图,到海岛景区C有两条旅游线路可供选择,游人可从码头A乘游艇或从码头B乘游船前往,已知B在A南偏东60°方向,C位于A南偏东45°方向10海里处,且C在B正西方向,游艇的速度为每小时30海里,游船的速度为每小时13海里,问游客选择哪条线路用时较少?并说明理由.(参考数据:
如图,到海岛景区C有两条旅游线路可供选择,游人可从码头A乘游艇或从码头B乘游船前往,已知B在A南偏东60°方向,C位于A南偏东45°方向10海里处,且C在B正西方向,游艇的速度为每小时30海里,游船的速度为每小时13海里,问游客选择哪条线路用时较少?并说明理由.(参考数据:| 2 |
| 3 |
| 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
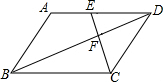 如图,在平行四边形ABCD中,点E是边AD上的一点,且AE:ED=2:3,EC交对角线BD于点F,则EF:FC等于( )
如图,在平行四边形ABCD中,点E是边AD上的一点,且AE:ED=2:3,EC交对角线BD于点F,则EF:FC等于( )| A、3:2 | B、2:5 |
| C、2:3 | D、3:5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、甲的够买方式合算 |
| B、乙的够买方式合算 |
| C、甲、乙的够买方式同样合算 |
| D、不能判断谁的够买方式合算 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com