
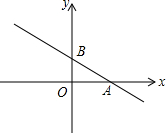
 如图,已知直线y=-$\frac{1}{2}$x+1分别交x轴、y轴于A、B两点,点M在x轴上,且满足
如图,已知直线y=-$\frac{1}{2}$x+1分别交x轴、y轴于A、B两点,点M在x轴上,且满足分析 由直线y=-$\frac{1}{2}$x+1分别求得x轴、y轴与A、B两点的坐标,得到AO,BO的长度,根据∠OMB+∠BAO=45°,画出图形,找到M点的位置,由勾股定理表示出BM,AM的长度,再根据相似三角形的性质,列出方程,求出结果.
解答 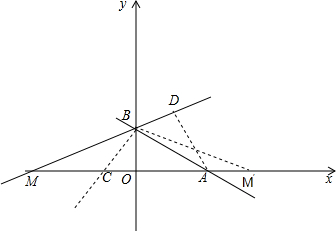 解:如图在y=-$\frac{1}{2}$x+1中,令y=0,得x=2,令x=0,y=1,
解:如图在y=-$\frac{1}{2}$x+1中,令y=0,得x=2,令x=0,y=1,
∴A(2,0),B(0,1),
∴OA=2,OB=1,
过点B作BC⊥AB,则∠ABC=∠CBE=90°,作∠EBC的平分线BM交x轴于M,∠ABC的平分线BM′交x轴于M′,
∴∠EBM=45°,即∠OMB+∠BAO=45°,
过点A作AD⊥MB交MB的延长线于点D,
∵∠ABD=∠DBA=45°,
∴OA=2,OB=1,
∴AB=$\sqrt{5}$,
∴AD=$\frac{\sqrt{10}}{2}$,
设OM=m,则BM=$\sqrt{{m}^{2}+1}$,
∵∠BMC=∠AMD,∠BOM=∠BDA,
∴△BCM∽△AMD,
∴$\frac{AM}{BM}$=$\frac{AD}{OB}$,即 $\frac{2+m}{\sqrt{{m}^{2}+1}}$=$\frac{\frac{\sqrt{10}}{2}}{1}$,
解得:m=3 m=$-\frac{2}{3}$(舍去),
点M关于y轴的对称点M′(3,0),也是满足条件的点.
M(-3,0),M′(3,O).
故答案(-3,0),(3,O).
点评 本题主要考查了利用函数解析式求点的坐标,相似三角形的判定和性质,角平分线的定义,三角形的外角的性质,此题的关键是画图找到M点的位置.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com