
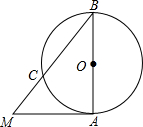
 已知:在⊙O中,AB是直径,AM与⊙O相切于点A,连接BM交⊙O于点C,若AM=6,半径为4,求BC的长.
已知:在⊙O中,AB是直径,AM与⊙O相切于点A,连接BM交⊙O于点C,若AM=6,半径为4,求BC的长. 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中数学 来源: 题型:
 某公园草坪的防护栏由100段形状相同的抛物线形构件组成,为了牢固起见,每段护栏需间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图所示),请计算所需不锈钢立柱的总长度.
某公园草坪的防护栏由100段形状相同的抛物线形构件组成,为了牢固起见,每段护栏需间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图所示),请计算所需不锈钢立柱的总长度.查看答案和解析>>
科目:初中数学 来源: 题型:
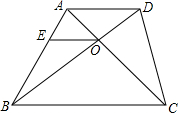 如图,在梯形ABCD中,AD∥BC,对角线AC与BD相交于点O,过点O作OE∥AD交AB于点E.若AD=6cm,BC=12cm,△AOD的面积为6cm2,
如图,在梯形ABCD中,AD∥BC,对角线AC与BD相交于点O,过点O作OE∥AD交AB于点E.若AD=6cm,BC=12cm,△AOD的面积为6cm2,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com