
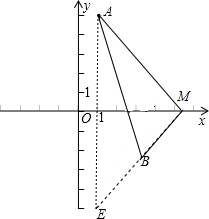
 解:作A关于x轴的对称点E,连接EB,延长EB交x轴于M,连接AM,则此时AM-BM的值最大,
解:作A关于x轴的对称点E,连接EB,延长EB交x轴于M,连接AM,则此时AM-BM的值最大,
|
| 3 |
| 2 |
| 13 |
| 2 |
| 3 |
| 2 |
| 13 |
| 2 |
| 3 |
| 2 |
| 13 |
| 2 |
| 13 |
| 3 |
| 13 |
| 3 |
| 13 |
| 3 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| 1 |
| 7 |
| 3 |
| 49 |
| 8 |
| 11 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 20 |
| 21 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 时间t(天) | 1 | 3 | 6 | … |
| 日销售量m(件) | 78 | 74 | 68 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 级别 | 全月应纳税所得额 | 税率(%) |
| 1 | 不超过1 500元的部分 | 3 |
| 2 | 超过1 500元不超过4 500元的部分 | 10 |
| 3 | 超过4 500元不超过9 000元的部分 | 20 |
| 4 | 超过9 000元不超过35 000元的部分 | 25 |
| … | … | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com