
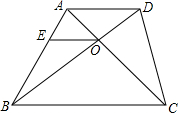
 如图,在梯形ABCD中,AD∥BC,对角线AC与BD相交于点O,过点O作OE∥AD交AB于点E.若AD=6cm,BC=12cm,△AOD的面积为6cm2,
如图,在梯形ABCD中,AD∥BC,对角线AC与BD相交于点O,过点O作OE∥AD交AB于点E.若AD=6cm,BC=12cm,△AOD的面积为6cm2,| OA |
| OC |
| OD |
| OB |
| AD |
| BC |
| 6cm |
| 12cm |
| 1 |
| 2 |
| S△AOD |
| S△BOC |
| 1 |
| 2 |
| S△AOD |
| S△DOC |
| AO |
| OC |
| 1 |
| 2 |
| OE |
| AD |
| BO |
| BD |
| 2 |
| 3 |
| OA |
| OC |
| OD |
| OB |
| AD |
| BC |
| 6cm |
| 12cm |
| 1 |
| 2 |
| S△AOD |
| S△BOC |
| 1 |
| 2 |
| S△AOD |
| S△DOC |
| AO |
| OC |
| 1 |
| 2 |
| OE |
| AD |
| BO |
| BD |
| 2 |
| 2+1 |
| 2 |
| 3 |


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
| 时间t(天) | 1 | 3 | 6 | … |
| 日销售量m(件) | 78 | 74 | 68 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
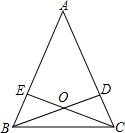 如图,已知AB=AC,AE=AD,则①△ABD≌△ACE,②△BOE≌△COD,③点O在∠BAC的平分线上,( )
如图,已知AB=AC,AE=AD,则①△ABD≌△ACE,②△BOE≌△COD,③点O在∠BAC的平分线上,( )| A、都正确 |
| B、都不正确 |
| C、只有一个正确 |
| D、只有一个不正确 |
查看答案和解析>>
科目:初中数学 来源: 题型:
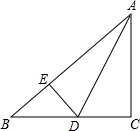 如图所示,已知AC⊥BC,AD平分∠BAC,DE⊥AB,那么下列等式不成立的是( )
如图所示,已知AC⊥BC,AD平分∠BAC,DE⊥AB,那么下列等式不成立的是( )| A、∠ADE=∠ADC |
| B、∠BAC=∠BDE |
| C、DC=DE |
| D、∠ADE=∠BDE |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com