
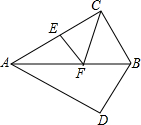
 两个全等的含30°的直角三角板如图放置(斜边重合),点E是AC的中点,AC=2,若点F是直线AB上的一个动点,则△CEF的周长最小值是
两个全等的含30°的直角三角板如图放置(斜边重合),点E是AC的中点,AC=2,若点F是直线AB上的一个动点,则△CEF的周长最小值是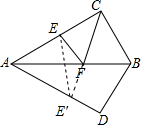 解:如图,过E作关于直线AB的对称点E′,连接CE′,由轴对称的性质可知CE′即为EF+FC的最小值,EF+FC的最小值=CE′,
解:如图,过E作关于直线AB的对称点E′,连接CE′,由轴对称的性质可知CE′即为EF+FC的最小值,EF+FC的最小值=CE′,| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 如图,在直角坐标系中,点A在x轴负半轴上,点B在x轴正半轴上,以线段AB为弦的⊙C与直线x=-2相切于点E(-2,
如图,在直角坐标系中,点A在x轴负半轴上,点B在x轴正半轴上,以线段AB为弦的⊙C与直线x=-2相切于点E(-2,| 5 |
| 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
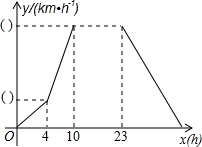 某气象研究中心观测一场沙尘暴从发生到结束的全过程.开始时风速平均每小时增加2km,4h后,沙尘暴经过开阔荒漠地,风速变为平均增加4km/h.一段时间,风速保持不变.当沙尘暴遇到绿色植被区时,其风速平均减小lkm/h,最终停止.结合风速y与时间x的图象(如图),回答下列问题.
某气象研究中心观测一场沙尘暴从发生到结束的全过程.开始时风速平均每小时增加2km,4h后,沙尘暴经过开阔荒漠地,风速变为平均增加4km/h.一段时间,风速保持不变.当沙尘暴遇到绿色植被区时,其风速平均减小lkm/h,最终停止.结合风速y与时间x的图象(如图),回答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:
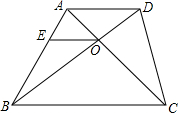 如图,在梯形ABCD中,AD∥BC,对角线AC与BD相交于点O,过点O作OE∥AD交AB于点E.若AD=6cm,BC=12cm,△AOD的面积为6cm2,
如图,在梯形ABCD中,AD∥BC,对角线AC与BD相交于点O,过点O作OE∥AD交AB于点E.若AD=6cm,BC=12cm,△AOD的面积为6cm2,查看答案和解析>>
科目:初中数学 来源: 题型:
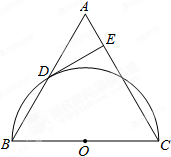 已知:如图,在△ABC中,AB=AC,以BC为直径的半圆O与边AB相交于点D,切线DE⊥AC,垂足为点E.求证:
已知:如图,在△ABC中,AB=AC,以BC为直径的半圆O与边AB相交于点D,切线DE⊥AC,垂足为点E.求证:| 1 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
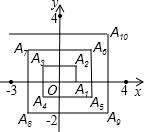 如图,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),…,则点A2013的坐标为( )
如图,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),…,则点A2013的坐标为( )| A、(504,-503) |
| B、(504,504) |
| C、(-504,504) |
| D、(-504,-504) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com