
ЁОЬтФПЁПЗжРрЬжТлЪЧвЛжжЗЧГЃживЊЕФЪ§бЇЗНЗЈЃЌШчЙћвЛЕРЬтЬсЙЉЕФвбжЊЬѕМўжаАќКЌМИжжЧщПіЃЌЮвУЧПЩвдЗжЧщПіЬжТлРДЧѓНт.Р§ШчЃКШє![]() ЃЌ
ЃЌ![]() Чѓ
Чѓ![]() ЕФжЕ.
ЕФжЕ.
ЧщПіШєx=3ЃЌy=2ЪБЃЌ![]() =5
=5
ЧщПіШєx=3ЃЌy=-2ЪБЃЌ![]() =1
=1
ЧщПіЂлШєx=-3ЃЌy=2ЪБЃЌ![]() =-1
=-1
ЧщПіЂмШєx=-3ЃЌy=-2ЪБЃЌ![]() =-5
=-5
ЫљвдЃЌ![]() ЕФжЕЮЊ1ЃЌ-1ЃЌ5ЃЌ-5.
ЕФжЕЮЊ1ЃЌ-1ЃЌ5ЃЌ-5.
МИКЮЕФбЇЯАЙ§ГЬжавВгаРрЫЦЕФЧщПі:
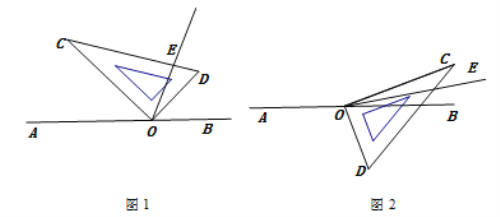
ШчЭМЃЌЕуOЪЧжБЯпABЩЯЕФвЛЕуЃЌНЋвЛжБНЧШ§НЧАхШчЭМАкЗХЃЌЙ§ЕуOзїЩфЯпOEЦНЗж![]() ЃЎЕБжБНЧШ§НЧАхШЦЕуOМЬајЫГЪБеыа§зЊвЛжмЛиЕНЭМ1ЕФЮЛжУЪБЃЌдка§зЊЙ§ГЬжаФуЗЂЯж
ЃЎЕБжБНЧШ§НЧАхШЦЕуOМЬајЫГЪБеыа§зЊвЛжмЛиЕНЭМ1ЕФЮЛжУЪБЃЌдка§зЊЙ§ГЬжаФуЗЂЯж![]() гыЁЯDOEЃЈ
гыЁЯDOEЃЈ![]() ЃЌ
ЃЌ![]() ЃЉжЎМфгадѕбљЕФЪ§СПЙиЯЕЃП
ЃЉжЎМфгадѕбљЕФЪ§СПЙиЯЕЃП
ЧщПіЃЈ1ЃЉШчЭМ1ЃЌЕБ![]() ЪБЃЌШє
ЪБЃЌШє![]() ЃЌдђЁЯDOEЖШЪ§ЪЧ
ЃЌдђЁЯDOEЖШЪ§ЪЧ
ЧщПіЃЈ2ЃЉШчЭМ2ЃЌЕБЁЯAOCЪЧЖлНЧЪБЃЌЪЙЕУжБНЧБпOCдкжБЯпABЕФЩЯЗНЃЌШєЁЯAOC=160ЁуЃЌЦфЫћЬѕМўВЛБфЃЌдђЁЯDOEЕФЖШЪ§ЪЧ
ЧщПіЃЈ3ЃЉШє![]() ЃЌдка§зЊЙ§ГЬжаФуЗЂЯж
ЃЌдка§зЊЙ§ГЬжаФуЗЂЯж![]() гыЁЯDOEжЎМфгадѕбљЕФЪ§СПЙиЯЕЃПЧыФужБНггУКЌІСЕФДњЪ§ЪНБэЪОЁЯDOEЕФЖШЪ§ЃЛ
гыЁЯDOEжЎМфгадѕбљЕФЪ§СПЙиЯЕЃПЧыФужБНггУКЌІСЕФДњЪ§ЪНБэЪОЁЯDOEЕФЖШЪ§ЃЛ
ЁОД№АИЁПЃЈ1ЃЉ20ЖШЃЛЃЈ2ЃЉ80ЖШЃЛЃЈ3ЃЉЕБOCдкABЩЯЗНЪБЃЌЁЯDOEЕФЖШЪ§ЪЧ![]() ЃЌЕБOCдкABЯТЗНЪБЃЌЁЯDOEЕФЖШЪ§ЪЧ
ЃЌЕБOCдкABЯТЗНЪБЃЌЁЯDOEЕФЖШЪ§ЪЧ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉШчЭМ1,ИљОнНЧЦНЗжЯпЕУЁЯCOE=70Ёу,РћгУШ§НЧАхЕУЁЯCOD=90Ёу,МДПЩНтЬт,ЃЈ2ЃЉИљОнНЧЦНЗжЯпЕУЁЯCOE=10Ёу,РћгУШ§НЧАхЕУЁЯCOD=90Ёу,МДПЩНтЬт,ЃЈ3ЃЉЕБOCдкABЩЯЗНЪБКЭOCдкABЯТЗНЪБЃЌЗжРрЬжТлМДПЩЧѓНт.
НтЃКЃЈ1ЃЉШчЭМ1,ЁпЁЯAOC=40Ёу,
ЁрЁЯBOC=140Ёу,
ЁпOEЦНЗж![]() ,
,
ЁрЁЯCOE=70Ёу,
ЁрЁЯDOE=90Ёу-70Ёу=20Ёу,
ЃЈ2ЃЉШчЭМ2,ЭЌРэПЩжЄ
ЁЯBOC=20Ёу,
ЁпOEЦНЗж![]() ,
,
ЁрЁЯCOE=10Ёу,
ЁрЁЯDOE=90Ёу-10Ёу=80Ёу,
ЃЈ3ЃЉЭЌЧАСНЮЪ,ЕБOCдкABЩЯЗНЪБЃЌЁЯDOEЕФЖШЪ§=![]() ЃЌ
ЃЌ
РэгЩШчЭМ1, ЁпЁЯAOC=ІС,
ЁрЁЯBOC=180Ёу-ІС,
ЁпOEЦНЗж![]() ,
,
ЁрЁЯCOE=90Ёу-![]() ,
,
ЁрЁЯDOE=90Ёу-ЃЈ90Ёу-![]() ЃЉ=
ЃЉ=![]() ,
,
ЭЌРэЃКЕБOCдкABЯТЗНЪБЃЌЁЯDOEЕФЖШЪ§=![]() .
.


 УћаЃЭЈаажЄгааЇзївЕЯЕСаД№АИ
УћаЃЭЈаажЄгааЇзївЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГжабЇгаШєИЩЬзЫ№ЛЕЕФзРвЮЃЌЯжгаМзЁЂввСНУћФОЙЄЃЌМзУПЬьПЩвдаозРвЮ16ЬзЃЌввУПЬьБШМзЖраозРвЮ8ЬзЃЌМзЕЅЖРаоЭъетаЉзРвЮБШввЕЅЖРаоЭъЖргУ10ЬьЃЌбЇаЃУПЬьИЖМз80дЊаоРэЗбЃЌИЖвв120дЊаоРэЗбЃЎ
ЃЈ1ЃЉетХњЫ№ЛЕЕФзРвЮгаЖрЩйЬзЃПЃЈСаЗНГЬНтД№ЃЉ
ЃЈ2ЃЉдкаоРэЙ§ГЬжаЃЌбЇаЃвЊХЩвЛУћЙЄзїШЫдБНјаажЪСПМрЖНЃЌбЇаЃИКЕЃЫћУПЬь30дЊЩњЛюВЙжњЗбЃЌЯжгаСНжжаоРэЗНАИЃК
ЂйгЩввЕЅЖРаоРэЃЛ
ЂкМзЁЂввКЯзїЭЌЪБаоРэЃЎ
ФуШЯЮЊФФжжЗНАИЪЁЧЎЃПЪдЭЈЙ§МЦЫуЫЕУїЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЕБ![]() ЁмxЁм2ЪБЃЌКЏЪ§y=Љ2x+bЕФЭМЯѓЩЯжСЩйгавЛЕудкКЏЪ§y=
ЁмxЁм2ЪБЃЌКЏЪ§y=Љ2x+bЕФЭМЯѓЩЯжСЩйгавЛЕудкКЏЪ§y=![]() ЕФЭМЯѓЯТЗНЃЌдђbЕФШЁжЕЗЖЮЇЮЊЃЈЁЁЁЁЃЉ
ЕФЭМЯѓЯТЗНЃЌдђbЕФШЁжЕЗЖЮЇЮЊЃЈЁЁЁЁЃЉ
A. b![]() B. bЃМ
B. bЃМ![]() C. bЃМ3 D. 2
C. bЃМ3 D. 2![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЭМАИжаМШЪЧжааФЖдГЦЭМаЮЃЌгжЪЧжсЖдГЦЭМаЮЕФЪЧЃЈ ЃЉ
A. ![]() B.
B.  C.
C.  D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=ax2+bxЉ3ОЙ§ЕуAЃЈ2ЃЌЉ3ЃЉЃЌгыxжсИКАыжсНЛгкЕуBЃЌгыyжсНЛгкЕуCЃЌЧвOC=3OBЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕуDдкyжсЩЯЃЌЧвЁЯBDO=ЁЯBACЃЌЧѓЕуDЕФзјБъЃЛ
ЃЈ3ЃЉЕуMдкХзЮяЯпЩЯЃЌЕуNдкХзЮяЯпЕФЖдГЦжсЩЯЃЌЪЧЗёДцдквдЕуAЃЌBЃЌMЃЌNЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃПШєДцдкЃЌЧѓГіЫљгаЗћКЯЬѕМўЕФЕуMЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЦпФъМЖбЇЩњГЫГЕШЅВЮМгЩчЛсЪЕМљЛАЖЏЃЌШєУПСОПЭГЕГЫ50ШЫЃЌЛЙга12ШЫВЛФмЩЯГЕЃЛШєУПСОПЭГЕГЫ55ШЫЃЌдђзюКѓвЛСОПеСЫ8ИізљЮЛЃЌЧѓИУаЃзтСЫЖрЩйСОПЭГЕЃПЦпФъМЖбЇЩњЖрЩйШЫЃП
ИљОнЬтвтЃЌаЁУїЁЂаЁКьЗжБ№СаГіСЫЩаВЛЭъећЕФЗНГЬШчЯТЃК
аЁУїЃК50xПк![]() ЁЁЁЁ
ЁЁЁЁ![]() Пк
Пк![]() ЁЁЁЁ
ЁЁЁЁ![]() ЃЛаЁКьЃК
ЃЛаЁКьЃК![]()
ЃЈЦфжаЁАПкЁББэЪОдЫЫуЗћКХЃЌЁА![]() ЁЁЁЁ
ЁЁЁЁ![]() ЁББэЪОЪ§зжЃЉ
ЁББэЪОЪ§зжЃЉ
![]() аЁУїЫљСаЗНГЬжаxБэЪОЕФвтвхЪЧЃК______ЃЛаЁКьЫљСаЗНГЬжаyБэЪОЕФвтвхЪЧЃК______ЃЛ
аЁУїЫљСаЗНГЬжаxБэЪОЕФвтвхЪЧЃК______ЃЛаЁКьЫљСаЗНГЬжаyБэЪОЕФвтвхЪЧЃК______ЃЛ
![]() ЧыФуАбаЁУїЛђаЁКьЫљСаЗНГЬВЙГфЭъећЃЌВЂЯргІНтД№ЃЎ
ЧыФуАбаЁУїЛђаЁКьЫљСаЗНГЬВЙГфЭъећЃЌВЂЯргІНтД№ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЦНааЫФБпаЮABCDШЦЕуAФцЪБеыа§зЊ30ЁуЃЌЕУЕНЦНааЫФБпаЮABЁфCЁфDЁфЃЈЕуBЁфгыЕуBЪЧЖдгІЕуЃЌЕуCЁфгыЕуCЪЧЖдгІЕуЃЌЕуDЁфгыЕуDЪЧЖдгІЕуЃЉЃЌЕуBЁфЧЁКУТфдкBCБпЩЯЃЌдђЁЯCЕФЖШЪ§ЕШгкЃЈЁЁЁЁЃЉ
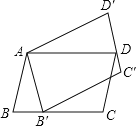
A. 100Ёу B. 105Ёу C. 115Ёу D. 120Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхЃКЖдгквЛИігаРэЪ§xЃЌЮвУЧАб[x]ГЦзїxЕФЖдГЦЪ§.
Шє![]() ЃЌдђ[x]=x-2:Шєx<0ЃЌдђ[x]=x+2.Р§ЃК[1]=1-2=-1ЃЌ[-2]=-2+2=0
ЃЌдђ[x]=x-2:Шєx<0ЃЌдђ[x]=x+2.Р§ЃК[1]=1-2=-1ЃЌ[-2]=-2+2=0
ЃЈ1ЃЉЧѓ[![]() ][-1]ЕФжЕЃЛ
][-1]ЕФжЕЃЛ
ЃЈ2ЃЉвбжЊгаРэЪ§a>0.b<0ЃЌЧвТњзу[a]=[b]ЃЌЪдЧѓДњЪ§ЪН![]() ЕФжЕЃК
ЕФжЕЃК
ЃЈ3ЃЉНтЗНГЬЃК[2x]+[x+1]=1
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЗНЗЈИаЮђЃК
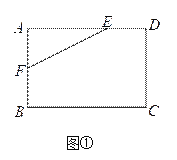
ЃЈ1ЃЉШчЭМЂйЃЌдкОиаЮABCDжаЃЌAB=4ЃЌAD=6ЃЌAE=4ЃЌAF=2ЃЌЪЧЗёдкБпBCЁЂCDЩЯЗжБ№ДцдкЕуGЁЂHЃЌЪЙЕУЫФБпаЮEFGHЕФжмГЄзюаЁЃПШєДцдкЃЌЧѓГіЫќжмГЄЕФзюаЁжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЮЪЬтНтОіЃК
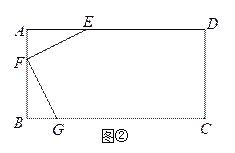
ЃЈ2ЃЉШчЭМЂкЃЌгавЛОиаЮАхВФABCDЃЌAB=3УзЃЌAD=6УзЃЌЯжЯыДгДЫАхВФжаВУГівЛИіУцЛ§ОЁПЩФмДѓЕФЫФБпаЮEFGHВПМўЃЌЪЙЁЯEFG=90ЁуЃЌEF=FG=![]() УзЃЌЁЯEHG=45ЁуЃЌОбаОПЃЌжЛгаЕБЕуEЁЂFЁЂGЗжБ№дкБпADЁЂABЁЂBCЩЯЃЌЧвAFЃМBFЃЌВЂТњзуЕуHдкОиаЮABCDФкВПЛђБпЩЯЪБЃЌВХгаПЩФмВУГіЗћКЯвЊЧѓЕФВПМўЃЌЪдЮЪФмЗёВУЕУЗћКЯвЊЧѓЕФУцЛ§ОЁПЩФмДѓЕФЫФБпаЮEFGHВПМўЃПШєФмЃЌЧѓГіВУЕУЕФЫФБпаЮEFGHВПМўЕФУцЛ§ЃЌВЂаДГідквдBЮЊзјБъдЕуЃЌжБЯпBCЮЊxжсЃЌжБЯпBAЮЊyжсЕФзјБъЯЕжаЃЌЕуHЕФзјБъЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
УзЃЌЁЯEHG=45ЁуЃЌОбаОПЃЌжЛгаЕБЕуEЁЂFЁЂGЗжБ№дкБпADЁЂABЁЂBCЩЯЃЌЧвAFЃМBFЃЌВЂТњзуЕуHдкОиаЮABCDФкВПЛђБпЩЯЪБЃЌВХгаПЩФмВУГіЗћКЯвЊЧѓЕФВПМўЃЌЪдЮЪФмЗёВУЕУЗћКЯвЊЧѓЕФУцЛ§ОЁПЩФмДѓЕФЫФБпаЮEFGHВПМўЃПШєФмЃЌЧѓГіВУЕУЕФЫФБпаЮEFGHВПМўЕФУцЛ§ЃЌВЂаДГідквдBЮЊзјБъдЕуЃЌжБЯпBCЮЊxжсЃЌжБЯпBAЮЊyжсЕФзјБъЯЕжаЃЌЕуHЕФзјБъЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com