
如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=
 (k>0,x>0)的图象上,点D的坐标为(4,3).
(k>0,x>0)的图象上,点D的坐标为(4,3).
(1)求k的值;
(2)若将菱形ABCD沿x轴正方向平移,当菱形的顶点D落在函数y=
 (k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.
(k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.


【考点】反比例函数综合题.
【分析】(1)过点D作x轴的垂线,垂足为F,首先得出A点坐标,再利用反比例函数图象上点的坐标性质得出即可;
(2)将菱形ABCD沿x轴正方向平移,使得点D落在函数
 (x>0)的图象D′点处,得出点D′的纵坐标为3,求出其横坐标,进而得出菱形ABCD平移的距离.
(x>0)的图象D′点处,得出点D′的纵坐标为3,求出其横坐标,进而得出菱形ABCD平移的距离.
【解答】解:(1)过点D作x轴的垂线,垂足为F,
∵点D的坐标为(4,3),
∴OF=4,DF=3,
∴OD=5,
∴AD=5,
∴点A坐标为(4,8),
∴k=xy=4×8=32,
∴k=32;
(2)将菱形ABCD沿x轴正方向平移,使得点D落在函数
 (x>0)的图象D′点处,
(x>0)的图象D′点处,
过点D′做x轴的垂线,垂足为F′.
∵DF=3,
∴D′F′=3,
∴点D′的纵坐标为3,
∵点D′在
 的图象上
的图象上
∴3=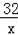
 ,
,
解得:x=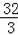
 ,
,
即OF′=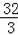
 ,
,
∴FF′=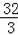
 ﹣4=
﹣4=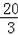
 ,
,
∴菱形ABCD平移的距离为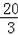
 .
.


【点评】此题主要考查了反比例函数综合以及反比例函数图象上点的坐标性质,得出A点坐标是解题关键.


科目:初中数学 来源: 题型:
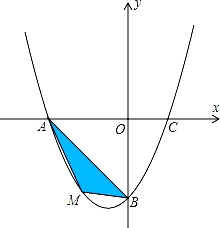
在平面直角坐标系中,已知抛物线y=ax2+bx﹣4经过A(﹣4,0),C(2,0)两点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值;
(3)若点P是抛物线上的动点,点Q是直线y=﹣x上的动点,点B是抛物线与y轴交点.判断有几个位置能够使以点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
某中学九(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题:
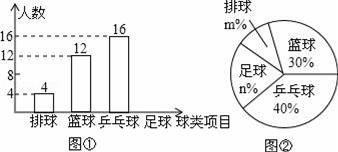

(1)九(1)班的学生人数为 ,并把条形统计图补充完整;
(2)扇形统计图中m= ,n= ,表示“足球”的扇形的圆心角是 度;
(3)排球兴趣小组4名学生中有3男1女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
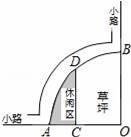
如图是某公园的一角,∠AOB=90°,弧AB的半径OA长是6米,C是OA的中点,点D在弧AB上,CD∥OB,则图中休闲区(阴影部分)的面积是( )

A.(10π﹣
 )米2 B.(π﹣
)米2 B.(π﹣
 )米2 C.(6π﹣
)米2 C.(6π﹣
 )米2 D.(6π﹣
)米2 D.(6π﹣
 )米2
)米2
查看答案和解析>>
科目:初中数学 来源: 题型:
为了估计某市空气质量情况,某同学在30天里做了如下记录:
| 污染指数(w) | 40 | 60 | 80 | 100 | 120 | 140 |
| 天数(天) | 3 | 5 | 10 | 6 | 5 | 1 |
其中w<50时空气质量为优,50≤w≤100时空气质量为良,100<w≤150时空气质量为轻度污染,若1年按365天计算,请你估计该城市在一年中空气质量达到良以上(含良)的天数为 天.
查看答案和解析>>
科目:初中数学 来源: 题型:
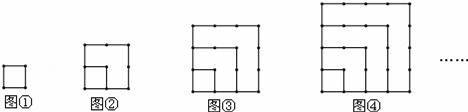
用火柴棍按下列方式摆图形,第1个图形用了4根火柴棍,第2个图形用了10根火柴棍,第3个图形用了18根火柴棍.依照此规律,若第n个图形用了88根火柴棍,则n的值为( )

A.6 B.7 C.8 D.9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com