
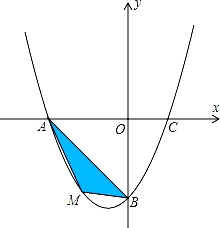
��ƽ��ֱ������ϵ�У���֪������y=ax2+bx��4����A����4��0����C��2��0�����㣮
��1���������ߵĽ���ʽ��
��2������MΪ������������������һ���㣬��M�ĺ�����Ϊm����AMB�����ΪS����S����m�ĺ�����ϵʽ�������S�����ֵ��
��3������P���������ϵĶ��㣬��Q��ֱ��y=��x�ϵĶ��㣬��B����������y�ύ�㣮�ж��м���λ���ܹ�ʹ�Ե�P��Q��B��OΪ������ı���Ϊƽ���ı��Σ�ֱ��д����Ӧ�ĵ�Q�����꣮
��
��
�����㡿���κ����ۺ��⣮
����������1���������߽���ʽΪy=ax2+bx+c��Ȼ��ѵ�A��B��C��������뺯������ʽ�����ô���ϵ������⼴�ɣ�
��2������ͼ�εĸ�����ɵö��κ��������������ߵ�����������������ڶ��κ�������ֵ��Ȼ�ɵý⣻
��3������ֱ���������ߵĽ���ʽ��ʾ����P��Q�����꣬Ȼ�����PQ�ij��ȣ��ٸ���ƽ���ı��εĶԱ�����г���ʽ��Ȼ������x��һԪ���η��̼��ɵý⣮
����𡿽⣺��1����A����4��0����C��2��0��������뺯������ʽ����

���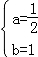
���Դ˺�������ʽΪ��y= x2+x��4��
x2+x��4��
��2����M��ĺ�����Ϊm���ҵ�M�������������ϣ�
��M�����������m�� m2+m��4����
m2+m��4����
��S=S��AOM+S��OBM��S��AOB
= ��4����
��4���� m2+m��4��+
m2+m��4��+ ��4������m����
��4������m���� ��4��4
��4��4
=��m2��2m+8��2m��8
=��m2��4m
=����m+2��2+4��
�ߩ�4��m��0��
��m=��2ʱ��S�����ֵΪ��S=��4+8=4��
��m=��2ʱS�����ֵS=4��
��3���ߵ�Q��ֱ��y=��x�ϵĶ��㣬
�����Q��������a����a����
�ߵ�P���������ϣ���PQ��y�ᣬ
���P��������a�� a2+a��4����
a2+a��4����
��PQ=��a���� a2+a��4��=��
a2+a��4��=�� a2��2a+4��
a2��2a+4��
�֡�OB=0������4��=4��
�Ե�P��Q��B��OΪ������ı�����ƽ���ı��Σ�
��|PQ|=OB��
��|�� a2��2a+4|=4��
a2��2a+4|=4��
�٩� a2��2a+4=4ʱ�������ã�a2+4a=0��
a2��2a+4=4ʱ�������ã�a2+4a=0��
���a=0����ȥ����a=��4��
��a=4��
���Ե�Q����Ϊ����4��4����
�ک� a2��2a+4=��4ʱ�������ã�a2+4a��16=0��
a2��2a+4=��4ʱ�������ã�a2+4a��16=0��
���a=��2��2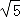 ��
��
���Ե�Q������Ϊ����2+2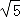 ��2��2
��2��2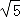 ����2��2
����2��2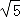 ��2+2
��2+2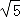 ����
����
����������Q��������4��4����2+2 ��2��2
��2��2 ����2��2
����2��2 ��2+2
��2+2 ��ʱ��ʹ��P��Q��B��OΪ������ı�����ƽ���ı��Σ�
��ʱ��ʹ��P��Q��B��OΪ������ı�����ƽ���ı��Σ�
�����������⿼���˶��κ����ۺ��⣬�д���ϵ��������κ�������ʽ������ͼ�θ���ó����κ�������ֵ�����ǽ���ؼ���ƽ���ı��εĶԱ���ȵ����ʣ�ƽ��ֱ������ϵ�������ľ���ı�ʾ���ۺ��Խ�ǿ�����ѶȲ�����ϸ�����㲻����⣮
��


 �п������п��Ծ����ϵ�д�
�п������п��Ծ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��֪����ABCD�У�AB=3cm��AD=4cm����AΪԲ�ģ�4cmΪ�뾶����A��������
A��B�ڡ�A�ڣ�C�ڡ�A�� B��D�ڡ�A�ڣ�C�ڡ�A��
C��B�ڡ�A�ڣ�D�ڡ�A�� D��B�ڡ�A�ϣ�C�ڡ�A��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
һ���ڴ������ĸ���ȫ��ͬ��С�����Ƿֱ���Ϊ1��2��3��4�����������һ��С��Ȼ��Żأ������������һ��С��������������С���ŵĺ͵���4�ĸ�������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
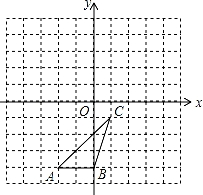
��ͼ����ABC�����������ֱ���A����2����4����B��0����4����C��1����1����
��1����ͼ�л�����ABC����ƽ��3����λ��ġ�A1B1C1��
��2����ͼ�л�����ABC��ԭ��O��ʱ����ת90���ġ�A2B2C2��
��3���ڣ�2���������£�AC��ɨ�����������������������
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
������һ��ֱ�ӡ��Բ�����������Ρ����Ρ����Ρ�������ͼ���Ŀ�Ƭ����Ƭ�г�ͼ����ͬ�⣬�������ͬ�����ֽ���ͼ����һ�泯������ڷţ����������ȡһ�ţ��鵽�����ĶԳ�ͼ���Ŀ�Ƭ�ĸ����ǣ�������
A�� B��
B�� C��
C�� D��
D��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ����O�İ뾶OD����AB�ڵ�C������AO���ӳ�����O�ڵ�E������EC����AB=8��CD=2����EC�ij�Ϊ��������������
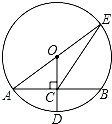
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
һ�������ɶ����ȫ��ͬ��С��������ɣ���������ͼ��ͼ��ʾ����ô�����������С������ĸ���Ϊ��������
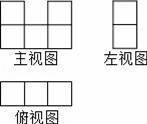

A��2�� B��3�� C��5�� D��10��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ����ƽ��ֱ������ϵ�У�����ABCD�Ķ���C��ԭ��O�غϣ���B��y����������ϣ���A�ڷ���������y=
 ��k��0��x��0����ͼ���ϣ���D������Ϊ��4��3����
��k��0��x��0����ͼ���ϣ���D������Ϊ��4��3����
��1����k��ֵ��
��2����������ABCD��x��������ƽ�ƣ������εĶ���D���ں���y=
 ��k��0��x��0����ͼ����ʱ��������ABCD��x��������ƽ�Ƶľ��룮
��k��0��x��0����ͼ����ʱ��������ABCD��x��������ƽ�Ƶľ��룮


��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com