
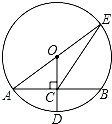
如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为 .
2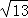
 .
.
【考点】垂径定理;勾股定理;三角形中位线定理;圆周角定理.
【专题】计算题.
【分析】连结BE,设⊙O的半径为R,由OD⊥AB,根据垂径定理得AC=BC=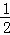 AB=4,在Rt△AOC中,OA=R,OC=R﹣CD=R﹣2,根据勾股定理得到(R﹣2)2+42=R2,解得R=5,则OC=3,由于OC为△ABE的中位线,则BE=2OC=6,再根据圆周角定理得到∠ABE=90°,然后在Rt△BCE中利用勾股定理可计算出CE.
AB=4,在Rt△AOC中,OA=R,OC=R﹣CD=R﹣2,根据勾股定理得到(R﹣2)2+42=R2,解得R=5,则OC=3,由于OC为△ABE的中位线,则BE=2OC=6,再根据圆周角定理得到∠ABE=90°,然后在Rt△BCE中利用勾股定理可计算出CE.
【解答】解:连结BE,设⊙O的半径为R,如图,
∵OD⊥AB,
∴AC=BC=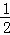 AB=
AB=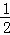 ×8=4,
×8=4,
在Rt△AOC中,OA=R,OC=R﹣CD=R﹣2,
∵OC2+AC2=OA2,
∴(R﹣2)2+42=R2,解得R=5,
∴OC=5﹣2=3,
∴BE=2OC=6,
∵AE为直径,
∴∠ABE=90°,
在Rt△BCE中,CE=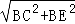 =
=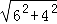 =2
=2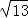 .
.
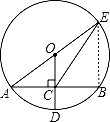
故答案为:2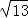 .
.
【点评】本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理、圆周角定理.


科目:初中数学 来源: 题型:
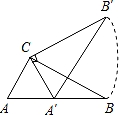
三角板ABC中,∠ACB=90°,∠B=30°,AC=2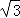 ,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边的起始位置上时即停止转动,则B点转过的路径长为( )
,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边的起始位置上时即停止转动,则B点转过的路径长为( )
A.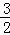 π B.
π B.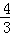
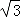 π C.2π D.3π
π C.2π D.3π
查看答案和解析>>
科目:初中数学 来源: 题型:
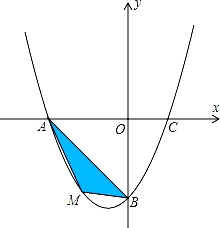
在平面直角坐标系中,已知抛物线y=ax2+bx﹣4经过A(﹣4,0),C(2,0)两点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值;
(3)若点P是抛物线上的动点,点Q是直线y=﹣x上的动点,点B是抛物线与y轴交点.判断有几个位置能够使以点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在长为8cm、宽为4cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下矩形的面积是( )

A.2cm2 B.4cm2 C.8cm2 D.16cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
某中学九(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题:
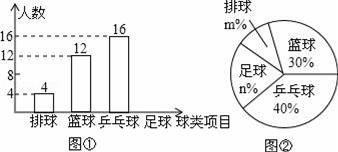

(1)九(1)班的学生人数为 ,并把条形统计图补充完整;
(2)扇形统计图中m= ,n= ,表示“足球”的扇形的圆心角是 度;
(3)排球兴趣小组4名学生中有3男1女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
用火柴棍按下列方式摆图形,第1个图形用了4根火柴棍,第2个图形用了10根火柴棍,第3个图形用了18根火柴棍.依照此规律,若第n个图形用了88根火柴棍,则n的值为( )
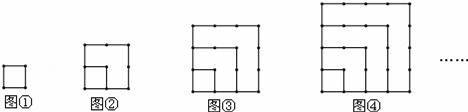

A.6 B.7 C.8 D.9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com