
分析 (1)根据平方差公式,可分母有理化;
(2)根据平方差公式,可分母有理化,根据实数的运算,可得答案.
解答 解:(1)$\frac{1}{{\sqrt{n}-\sqrt{n-1}}}$的结果为$\sqrt{n}$+$\sqrt{n-1}$,
故答案为:$\sqrt{n}$+$\sqrt{n-1}$;
(2)原式=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…+$\sqrt{99}$-$\sqrt{98}$+$\sqrt{100}$-$\sqrt{99}$
=$\sqrt{100}$-1
=9.
点评 本题考查了分母有理化,利用平方差公式是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
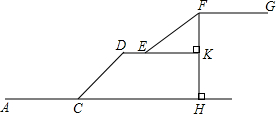 如图,校长寄语石到操场的垂直高度FH是30米,三教学楼到主席台的距离AC是60米,斜坡CD的坡脚是45°,斜坡EF的坡度i=3:4,公路宽DE与CH平行,且DE的延长线与FH的交点K,是FH中点,CH的长是40米,FG的长是50米.一名学生从三教学楼出发到行政楼交教学记录表,沿A-C-D-E-F-G路线,若上坡速度都为40米/分钟,平地速度都为50米/分钟,问该学生到达行政楼的时间是多少.($\sqrt{2}$≈1.4)
如图,校长寄语石到操场的垂直高度FH是30米,三教学楼到主席台的距离AC是60米,斜坡CD的坡脚是45°,斜坡EF的坡度i=3:4,公路宽DE与CH平行,且DE的延长线与FH的交点K,是FH中点,CH的长是40米,FG的长是50米.一名学生从三教学楼出发到行政楼交教学记录表,沿A-C-D-E-F-G路线,若上坡速度都为40米/分钟,平地速度都为50米/分钟,问该学生到达行政楼的时间是多少.($\sqrt{2}$≈1.4)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
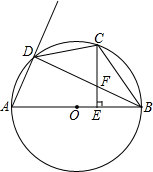 如图,AB是⊙O的直径,C是弧BD的中点,CE⊥AB,垂足为E,BD交CE于点F.
如图,AB是⊙O的直径,C是弧BD的中点,CE⊥AB,垂足为E,BD交CE于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
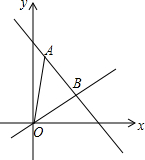 如图,在平面直角坐标系中,一次函数y=kx+5的图象经过点A(1,4),点B是一次函数y=kx+5的图象与正比例函数$y=\frac{2}{3}x$的图象的交点.
如图,在平面直角坐标系中,一次函数y=kx+5的图象经过点A(1,4),点B是一次函数y=kx+5的图象与正比例函数$y=\frac{2}{3}x$的图象的交点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
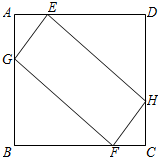 如图,边长为4的正方形ABCD中,AE=CF=1,点G、H分别是边AB、CD上的动点,且AG=CH.
如图,边长为4的正方形ABCD中,AE=CF=1,点G、H分别是边AB、CD上的动点,且AG=CH.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com