
如图,半圆的直径AB=10,C、D是半圆的三等分点,P为AB上一点,求阴影部分的面积.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
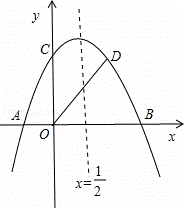
如图,抛物线 与x轴交于A、B两点(A点在B点左侧),与y轴交于点C,对称轴为直线
与x轴交于A、B两点(A点在B点左侧),与y轴交于点C,对称轴为直线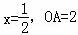 ,OD平分∠BOC交抛物线于点D(点D在第一象限).
,OD平分∠BOC交抛物线于点D(点D在第一象限).
(1)求抛物线的解析式和点D的坐标;
(2)在抛物线的对称轴上,是否存在一点P,使得△BPD的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
(3)点M是抛物线上的动点,在x轴上是否存在点N,使A、D、M、N四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的M点坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
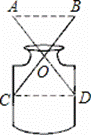
小红家有一个小口瓶(如图所示),她很想知道它的内径是多少?但是尺子不能伸在里边直接测,于是她想了想,唉!有办法了.她拿来了两根长度相同的细木条,并且把两根长木条的中点固定在一起,木条可以绕中点转动,这样只要量出AB的长,就可以知道玻璃瓶的内径是多少,你知道这是为什么吗?请说明理由.(木条的厚度不计)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com