
����Ŀ����ͼ1����PΪ��MON��ƽ������һ�㣬��PΪ����Ľǵ����߷ֱ�������OM��ON����A��B���㣬�����APB�Ƶ�P��תʱʼ������![]() �����ǾͰѡ�APB������MON���ǻ۽�.
�����ǾͰѡ�APB������MON���ǻ۽�.
��1����ͼ2����֪��MON=90������PΪ��MON��ƽ������һ�㣬�Ե�PΪ����Ľǵ����߷ֱ�������OM��ON����A��B���㣬�ҡ�APB=135��. ��֤����APB�ǡ�MON���ǻ۽ǣ�
��2����ͼ3��C�Ǻ���![]() ͼ���ϵ�һ�����㣬����C��ֱ��CD�ֱ�
ͼ���ϵ�һ�����㣬����C��ֱ��CD�ֱ�![]() ���
���![]() ���ڵ�A��B���㣬������BC=2CA���������AOB���ǻ۽ǡ�APB�Ķ���P������.
���ڵ�A��B���㣬������BC=2CA���������AOB���ǻ۽ǡ�APB�Ķ���P������.

���𰸡���1��֤������������2��![]() ��
��![]()
�������������������1���ɽ�ƽ���������AOP=��BOP=![]() ����MON=45������֤����OAP=��OPB���ó���Ӧ�߳ɱ���
����MON=45������֤����OAP=��OPB���ó���Ӧ�߳ɱ���![]() ���ó�OP2=OAOB�����ɵó����ۣ�
���ó�OP2=OAOB�����ɵó����ۣ�
��2�����C��a��b������ab=3������C��CH��OA��H�������������
�ٵ���B��y����������ʱ������A��x��ĸ�������ʱ��BC=2CA�����ܣ�����A��x�����������ʱ�������![]() ����ƽ���ߵó���ACH�ס�ABO���ó�����ʽ��
����ƽ���ߵó���ACH�ס�ABO���ó�����ʽ��
![]() ���ó�OB=3b��OA=
���ó�OB=3b��OA=![]() a�����OAOB=
a�����OAOB=![]() �����ݡ�APB�ǡ�AOB���ǻ۽ǣ��ó�OP�����ɵó���P�����ꣻ
�����ݡ�APB�ǡ�AOB���ǻ۽ǣ��ó�OP�����ɵó���P�����ꣻ
�ڵ���B��y��ĸ�������ʱ��������ó���AB=CA����AAS֤����ACH�ա�ABO���ó�OB=CH=b��OA=AH=![]() a���ó�OAOB=
a���ó�OAOB=![]() �����OP�����ɵó���P�����꣮
�����OP�����ɵó���P�����꣮
�⣺(1)֤�����ߡ�MON=90�㣬PΪ��MON��ƽ������һ�㣬
���AOP=��BOP=![]() ��MON=45�㣬
��MON=45�㣬
�ߡ�AOP+��OAP+��APO=180�㣬
���OAP+��APO=135�㣬
�ߡ�APB=135�㣬
���APO+��OPB=135�㣬
���OAP=��OPB��
����AOP����POB��
��![]() ��
��
��OP2=OAOB��
���APB�ǡ�MON���ǻ۽ǣ�
(2)���C(a,b)����ab=3��
����C��CH��OA��H�������������
�ٵ���B��y����������ʱ����A��x��ĸ�������ʱ����ͼ2:
BC=2CA������;
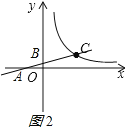
����A��x�����������ʱ����ͼ3:
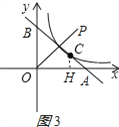
��BC=2CA��
��![]() ��
��
��CH��OB��
����ACH����ABO��
��![]() ,
,
��OB=3b,OA=![]() a��
a��
��OAOB=![]() a3b=
a3b=![]() ab=
ab=![]() ��
��
�ߡ�APB�ǡ�AOB���ǻ۽ǣ�
��OP=![]() ��
��
�ߡ�AOB=90�㣬OPƽ�֡�AOB��
���P��x,y��ľ������Ϊ![]()
���P��������![]() ��
��
�ڵ���B��y��ĸ�������ʱ,��ͼ4,
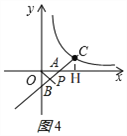
��BC=2CA��
��AB=CA��
�ߡ�AHC=��AOB=90�㣬
�֡ߡ�BAO=��CAH,
����ACH����ABO(AAS)��
��OB=CH=b,OA=AH=![]() a��
a��
��OAOB=![]() ab=
ab=![]() ��
��
�ߡ�APB�ǡ�AOB���ǻ۽ǣ�
��OP=![]()
�ߡ�AOB=90�㣬OPƽ�֡�AOB��
���P��x,y��ľ������Ϊ![]() ��
��
���P��������![]() ��
��
������������P��������![]() ��
��![]() .
.


 ��ʦָ��һ��ͨϵ�д�
��ʦָ��һ��ͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ʽ�У�����Ӧ��ƽ���ʽ���м�����ǣ� ��
A.��-x+2y����2y+x��B.��x+y����x-y��C.��a-b����-a+b��D.��-2m+n����-2m-n��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ع�ѧϰ�����Ĺ��̣��ɺ����ı���ʽͨ���б�����㡢������������ͼ�������ú���ͼ���о����������ʣ������������Ҫ���ֵ���ѧ�����ǣ�������
A. ���� B. ��� C. ������ D. ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ֶ�����ijһ�����������7�棬��������ǩ�1�棬��һ����ֵ��²��ǣ�������
A.��8��
B.6��
C.7��
D.8��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����ĵ�λ�������Ϊ1.24��10��3��/����3 �� 1.24��10��3��С����ʾΪ�� ��
A.0.000124
B.0.0124
C.��0.00124
D.0.00124
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���y��ax2��bx��cͼ���һ���֣�ͼ�����A����3��0�����Գ���Ϊx����1�������ĸ����ۣ���b2 �� 4ac����2a��b=0����a��b��c=0����5a �� b��������ȷ�����У�������

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���y=ax2+bx+c��ͼ���һ���֣��Գ�����ֱ��x=1��
��b2��4ac�� ��4a-2b+c��0�� �۲���ʽax2+bx+c��0�Ľ⼯��x��3.5�� ������-2��y1������5��y2�����������ϵ����㣬��y1��y2��
����4���ж��У���ȷ���ǣ�������
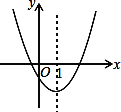
A. �٢� B. �٢� C. �٢ۢ� D. �ڢۢ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com