
����Ŀ����ƽ��ֱ������ϵxOy�У���P������Ϊ��x1��y1������Q������Ϊ��x2��y2������x1��x2��y1��y2����P��QΪij�����ε��������㣬�Ҹþ��εı߾���ij�������ᴹֱ����Ƹþ���Ϊ��P��Q�ġ���ؾ��Ρ�����ͼΪ��P��Q�ġ���ؾ��Ρ�ʾ��ͼ��
��1����֪��A������Ϊ��1��0����
������B������Ϊ��3��1�������A��B�ġ���ؾ��Ρ��������
�ڵ�C��ֱ��x=3�ϣ�����A��C�ġ���ؾ��Ρ�Ϊ�����Σ���ֱ��AC�ı���ʽ��
��2��������RSKT����R������Ϊ��-1��1����K������Ϊ��2��-2������M������Ϊ��m��3��������������RSKT���ϴ���һ��N��ʹ�õ�M��N�ġ���ؾ��Ρ�Ϊ�����Σ���m��ȡֵ��Χ��
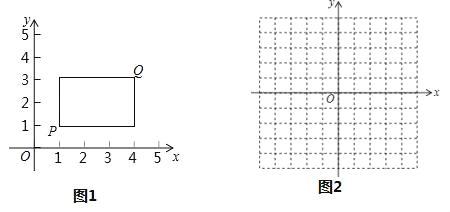
���𰸡���1����2����y=x��1��y=��x+1����2��1��m��7��0��m��6
�����������������
��1��������ؾ��εĶ����֪��Ҫ��A��B����ؾ����������AB��Ϊ�Խ��ߣ�����A��B��������꼴������þ��εĵ���ߵij��ȣ�����������þ��ε������
���ɶ����֪��AC��Ϊ�����εĶԽ��ߣ�����AC��x��ļнDZ�Ϊ45�㣬��ֱ��AC�Ľ���ʽΪ��y=kx+b���ɴ˿�֪k=��1���٣�1��0������y=kx+b���������b��ֵ��
��2���ɶ����֪��MN��Ϊ��ؾ��εĶԽ��ߣ�������ؾ��ε�Ϊ�����Σ���ֱ��MN��x��ļн�Ϊ45�㣬����ֱ��ƽ�п������m�ķ�Χ��
�����������1���١�A��1��0����B��3��1��
�ɶ����֪����A��B������ؾ������ĵ���߷ֱ�Ϊ2��1��
���A��B������ؾ����������Ϊ2��1=2��
���ɶ����֪��AC�ǵ�A��C������ؾ������ĶԽ��ߣ�
�֡ߵ�A��C������ؾ�����Ϊ������
��ֱ��AC��x��ļн�Ϊ45����
��ֱ��AC�Ľ���Ϊ��y=x+m��y=��x+n
�ѣ�1��0���ֱ�y=x+m��
��m=��1��
��ֱ��AC�Ľ���Ϊ��y=x��1��
�ѣ�1��0������y=��x+n��
��n=1��
��y=��x+1��
��������������A��C������ؾ�����Ϊ�����Σ�ֱ��AC�ı���ʽΪy=x��1��y=��x+1��
��2����ֱ��MN�Ľ���ʽΪy=kx+b��
�ߵ�M��N������ؾ�����Ϊ�����Σ�
���ɶ����֪��ֱ��MN��x��ļн�Ϊ45����
��k=��1��
�ߵ�N�������α��ϣ�
�൱ֱ��MN���������н���ʱ����M��N������ؾ�����Ϊ�����Σ�
��k=1ʱ��
����R��K��ֱ����ֱ��MNƽ�У�
����-1,1���ͣ�2��-2���ֱ����y=x+b
��b=2 ��b=-4
��M��m��3������y=x+2��y=x-4��
��m=1 m=7
��1��m��7��
��k=��1ʱ����(-1,-2) (2,1)����y=��x+b��
��b=-3 b=3��
��M��m��3������y=-x-3��y=-x+3��
��m=0 m=6
��0��m��6��
��������������M��N������ؾ�����Ϊ������ʱ��m��ȡֵ��Χ�ǣ�1��m��7��0��m��6


 ���������ν�ϵ�д�
���������ν�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������г��б�־�����������ں�������幫�ڣ���ͼ��Ϊ�˲����������ĸ߶�����E���ø�Ϊ1.5 m�IJ����AE���������C������Ϊ30�㣬��������ǰ��10.4 m���ֲ������C������Ϊ60�㣬���������ĸ߶ȣ�(�����ȷ��0.1 m)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��a��b��Ϊ��һ������һ�㣬��a��b������OA�����Ե�AΪ��ת���İ�OA��ʱ��ת90�����߶�BA������A��Bǡ�ö���ͬһ������������ͼ���ϣ���![]() ��ֵ����___��
��ֵ����___��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ö����ƽ���ֳ�����(ÿ������2ö)���ֱ������ߡ��м䡢�ұߣ���������˳����в���:
��1��:���ұ߶����ó� 2ö���ӷ����м�һ�ѣ�
��2��:�����һ�����ó�1ö���ӷ����м�һ�ѣ�
��3��:���м�һ�����ó���ö���ӷ����ұ�һ�ѣ���ʹ�ұ�һ�ѵ�������Ϊ�����2����
(1)�������������ұ߶ѱ����һ�Ѷ�15ö���ӣ��ʹ���_____ö���ӣ�
(2)ͨ������ó�:���������������Ϊ���٣�������������ɲ������м�һ������ʣ��_____ö���ӣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���![]() ������
������![]() �ύ��
�ύ��![]() ��
��![]() ����
����![]() ��
��![]() λ��ԭ�����࣬��
λ��ԭ�����࣬��![]() �������ύ��
�������ύ��![]() ������
������![]() ��
��![]() ���Ҳ��ֱ��
���Ҳ��ֱ��![]() ��
��![]() �ϣ�������˵������
�ϣ�������˵������![]() ��
��![]() ��
��![]() ��
��![]() ������ȷ�Ľ����У� ��
������ȷ�Ľ����У� ��

A.�٢�B.�ڢ�C.�٢ڢ�D.�٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���л��Ļ���ԴԶ����.����ѧ���棬�����μǡ����������塷��ˮ䰴�������¥�Ρ����ҹ��Ŵ���ƪС˵�еĵ��ʹ���������Ϊ���Ĵ�ŵ���������ij��ѧΪ���˽�ѧ�����Ĵ�ŵ��������Ķ�����������Ĵ�ŵ�����������˼�������������ȫУѧ���н����˳�������.���ݵ��������Ƴ�����ʾ��������������ͳ��ͼ������ͼ����Ϣ����������⣺
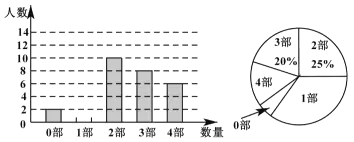
(1) ���ε���һ����ȡ��______��ѧ��������ͳ��ͼ����1�����������ε�Բ�Ľ�Ϊ______��
(2) ������ѧ��1000��ѧ��������������Ķ�3���Ĵ�ŵ�������ѧ���ж�������
(3) û�ж����Ĵ�����������ѧ�������Ĵ�ŵ������и������ѡ��һ�����Ķ���������ѡ��ͬһ�����ĸ���Ϊ_________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
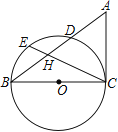
����Ŀ����ͼ��BC�ǡ�O��ֱ����AB����O�ڵ�D��EΪ��BD���е㣬CE��AB�ڵ�H��AC��AH
(1) ��֤��AC���O����
(2) ��CH��3EH����sin��ABC��ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ƽ��ֱ������ϵ�У�����OABC�ı�OA��OC�ֱ���x��������ᡢy����������ϣ���OA��OC��![]() ���ij��Ƿ���
���ij��Ƿ���![]() ����������
����������
��1����ͼ�����A�����ꣻ
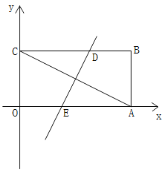
��2����ͼ��������OABC��ij��ֱ���۵���ʹ��A���C�غϣ��ۺ۽�CB�ڵ�D����OA�ڵ�E����ֱ��DE�Ľ���ʽ��

��3���ڣ�2���������£���P��ֱ��DE�ϣ���ֱ��AC���Ƿ���ڵ�Q��ʹ�Ե�A��B��P��QΪ������ı�����ƽ���ı��Σ������ڣ��������Q���ꣻ�������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��İְ����˽������·�ȥ�Ϻ����������һ����Ʊ����������˶�����ȥ�ۿ�������Ʊֻ��һ�ţ������꼶�ĸ������һ���취�����˰����˿��ƣ�������Ϊ1��2��3��5�������Ƹ�С������Ϊ4��6��7��8�������������Լ�������������Ϸ������У�С����Ӹ��Ե���������������һ�ţ�Ȼ����������˿���������ӣ������Ϊż������С��ȥ�������Ϊ����������ȥ��
��1��������״ͼ���б��ķ�����С��ȥ�Ϻ���������ĸ��ʣ�
��2�������Ƶ���Ϸ����ƽ������ƽ����˵�����ɣ�������ƽ���������һ�ֹ�ƽ����Ϸ����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com