
【题目】已知,在平面直角坐标系中,矩形OABC的边OA、OC分别在x轴的正半轴、y轴的正半轴上,且OA、OC(![]() )的长是方程
)的长是方程![]() 的两个根.
的两个根.
(1)如图,求点A的坐标;
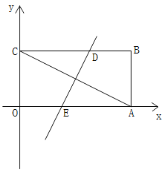
(2)如图,将矩形OABC沿某条直线折叠,使点A与点C重合,折痕交CB于点D,交OA于点E.求直线DE的解析式;

(3)在(2)的条件下,点P在直线DE上,在直线AC上是否存在点Q,使以点A、B、P、Q为顶点的四边形是平行四边形.若存在,请求出点Q坐标;若不存在,请说明理由.
【答案】(1)(8,0);(2)![]() ;(3)存在点
;(3)存在点![]() 或
或![]() 或
或![]() ,使以点A、B、P、Q为顶点的四边形是平行四边形.
,使以点A、B、P、Q为顶点的四边形是平行四边形.
【解析】
(1)通过解一元二次方程可求出OA的长,结合点A在x轴正半轴可得出点A的坐标;
(2)连接CE,设OE=m,则AE=CE=8-m,在Rt△OCE中,利用勾股定理可求出m的值,进而可得出点E的坐标,同理可得出点D的坐标,根据点D,E的坐标,利用待定系数法可求出直线DE的解析式;
(3)根据点A,C的坐标,利用待定系数法可求出直线AC的解析式,设点P的坐标为(a,2a-6),点Q的坐标为(c,-![]() c+4),分AB为边和AB为对角线两种情况考虑:①当AB为边时,利用平行四边形的性质可得出关于a,c的二元一次方程组,解之可得出c值,再将其代入点Q的坐标中即可得出结论;②当AB为对角线时,利用平行四边形的对角线互相平分,可得出关于a,c的二元一次方程组,解之可得出c值,再将其代入点Q的坐标中即可得出结论.综上,此题得解.
c+4),分AB为边和AB为对角线两种情况考虑:①当AB为边时,利用平行四边形的性质可得出关于a,c的二元一次方程组,解之可得出c值,再将其代入点Q的坐标中即可得出结论;②当AB为对角线时,利用平行四边形的对角线互相平分,可得出关于a,c的二元一次方程组,解之可得出c值,再将其代入点Q的坐标中即可得出结论.综上,此题得解.
(1)解方程x2-12x+32=0,得:x1=4,x2=8.
∵OA、OC的长是方程x2-12x+32=0的两个根,且OA>OC,点A在x轴正半轴上,
∴点A的坐标为(8,0).
(2)连接CE,如图4所示.

由(1)可得:点C的坐标为(0,4),点B的坐标为(8,4).
设OE=m,则AE=CE=8-m.
在Rt△OCE中,∠COE=90°,OC=4,OE=m,
∴CE2=OC2+OE2,即(8-m)2=42+m2,
解得:m=3,
∴OE=3,
∴点E的坐标为(3,0).
同理,可求出BD=3,
∴点D的坐标为(5,4).
设直线DE解析式为:![]()
![]()
∴![]()
∴直线DE解析式为:![]()
(3)∵点A的坐标为(8,0),点C的坐标为(0,4),点B的坐标为(8,4),
∴直线AC的解析式为y=-![]() x+4,AB=4.
x+4,AB=4.
设点P的坐标为(a,2a-6),点Q的坐标为(c,-![]() c+4).
c+4).
分两种情况考虑,如图5所示:
①当AB为边时,  ,
,
解得:c1=![]() ,c2=
,c2=![]() ,
,
∴点Q1的坐标为(![]() ,
,![]() ),点Q2的坐标为(
),点Q2的坐标为(![]() ,
,![]() );
);
②当AB为对角线时, ,
,
解得: ,
,
∴点Q3的坐标为(![]() ,-
,- ![]() ).
).
综上,存在点![]() 或
或![]() 或
或![]() ,使以点A、B、P、Q为顶点的四边形是平行四边形
,使以点A、B、P、Q为顶点的四边形是平行四边形



科目:初中数学 来源: 题型:
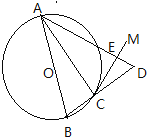
【题目】如图AB是△ABC的外接圆⊙O的直径,过点C作⊙O的切线CM,延长BC到点D,使CD=BC,连接AD交CM于点E,若⊙OD半径为3,AE=5,
(1)求证:CM⊥AD;
(2)求线段CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
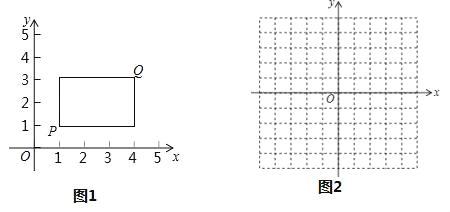
【题目】在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2,y1≠y2,若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”,如图为点P,Q的“相关矩形”示意图.
(1)已知点A的坐标为(1,0),
①若点B的坐标为(3,1),求点A,B的“相关矩形”的面积;
②点C在直线x=3上,若点A,C的“相关矩形”为正方形,求直线AC的表达式;
(2)正方形RSKT顶点R的坐标为(-1,1),K的坐标为(2,-2),点M的坐标为(m,3),若在正方形RSKT边上存在一点N,使得点M,N的“相关矩形”为正方形,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问 有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12 里,13 里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里=0.5千米,则该沙田的面积为( ) 平方千米.
A.7.5B.15C.75D.750
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习有理数得乘法后,老师给同学们这样一道题目:
计算:49![]() ×(﹣5),看谁算的又快又对,有两位同学的解法如下:
×(﹣5),看谁算的又快又对,有两位同学的解法如下:
聪聪:原式=﹣![]() ×5=﹣
×5=﹣![]() =﹣249
=﹣249![]() ;
;
明明:原式=(49+![]() )×(﹣5)=49×(﹣5)+
)×(﹣5)=49×(﹣5)+![]() ×(﹣5)=﹣249
×(﹣5)=﹣249![]() ;
;
(1)对于以上两种解法,你认为谁的解法较好?
(2)上面的解法对你有何启发,你认为还有更好的方法吗?如果有,请把它写出来;
(3)用你认为最合适的方法计算:29![]() ×(﹣8)
×(﹣8)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
已知:如图,在正方形ABCD中,边![]() .
.
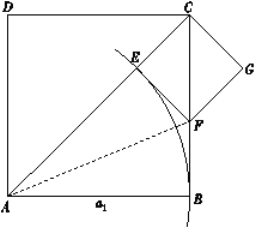
按照以下操作步骤,可以从该正方形开始,构造一系列的正方形,它们之间的边满足一定的关系,并且一个比一个小.
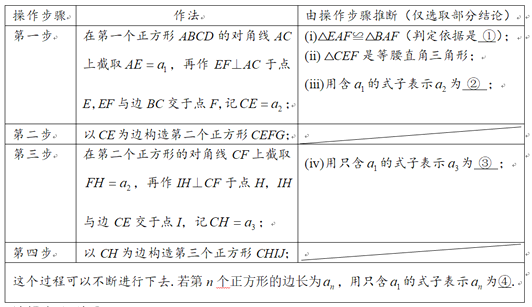
请解决以下问题:
(1)完成表格中的填空:
① ;② ;
③ ;④ ;
(2)根据以上第三步、第四步的作法画出第三个正方形CHIJ(不要求尺规作图).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“垃圾分一分,环境美十分”.甲、乙两城市产生的不可回收垃圾需运送到![]() 、
、![]() 两垃圾场进行处理,其中甲城市每天产生不可回收垃圾
两垃圾场进行处理,其中甲城市每天产生不可回收垃圾![]() 吨,乙城市每天产生不可回收垃圾
吨,乙城市每天产生不可回收垃圾![]() 吨。
吨。![]() 、
、![]() 两垃圾场每天各能处理
两垃圾场每天各能处理![]() 吨不可回收垃圾。从
吨不可回收垃圾。从![]() 垃圾处理场到甲城市
垃圾处理场到甲城市![]() 千米,到乙城市
千米,到乙城市![]() 千米;从
千米;从![]() 垃圾处理场到甲城市
垃圾处理场到甲城市![]() 千米,到乙城市
千米,到乙城市![]() 千米。
千米。
(1)请设计一个运输方案使垃圾的运输量(吨.千米)尽可能小;
(2)因部分道路维修,造成运输量不低于![]() 吨,请求出此时最合理的运输方案.
吨,请求出此时最合理的运输方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有个填写运算符号的游戏:在“![]() ”中的每个□内,填入
”中的每个□内,填入![]() 中的某一个(可重复使用),然后计算结果.
中的某一个(可重复使用),然后计算结果.
(1)计算:![]() ;
;
(2)若请推算![]() □内的符号;
□内的符号;
(3)在“![]() ”的□内填入符号后,使计算所得数最小,直接写出这个最小数.
”的□内填入符号后,使计算所得数最小,直接写出这个最小数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级![]() 班有
班有![]() 人,
人,![]() 班比
班比![]() 班人数的2倍少8人,如果从
班人数的2倍少8人,如果从![]() 班调出6人到
班调出6人到![]() 班.
班.
(1)用代数式表示两个班共有多少人?
(2)用代数式表示调动后,![]() 班人数比
班人数比![]() 班人数多几人?
班人数多几人?
(3)![]() 等于多少时,调动后两班人数一样多?
等于多少时,调动后两班人数一样多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com