练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问 有沙田一块，有三斜，其中小斜五里，中斜十二里,大斜十三里，欲知为田几何?”这道题讲的是:有一块三角形沙田，三条边长分别为5里，12 里，13 里，问这块沙田面积有多大?题中“里”是我国市制长度单位，1里=0.5千米，则该沙田的面积为( ) 平方千米.

    A.7.5B.15C.75D.750

    【答案】A

    【解析】

    直接利用勾股定理的逆定理进而结合直角三角形面积求法得出答案．

    解：∵52+122=132，
    ∴三条边长分别为5里，12里，13里，构成了直角三角形，
    ∴这块沙田面积为：×5×500×12×500=7500000（平方米）=7.5（平方千米）．
    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】（1）化简：（+1）÷，并从﹣1、0、1、2这四个数中选取一个合适的数作为x的值代入求值．

    （2）解方程： +2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将若干枚棋子平均分成三堆(每堆至少2枚)，分别放在左边、中间、右边，并按如下顺序进行操作:

    第1次:从右边堆中拿出 2枚棋子放入中间一堆；

    第2次:从左边一堆中拿出1枚棋子放入中间一堆；

    第3次:从中间一堆中拿出几枚棋子放入右边一堆，并使右边一堆的棋子数为最初的2倍．

    (1)操作结束后，若右边堆比左边一堆多15枚棋子，问共有_____枚棋子；

    (2)通过计算得出:无论最初的棋子数为多少，按上述方法完成操作后，中间一堆总是剩下_____枚棋子．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】中华文化，源远流长.在文学方面，《西游记》《三国演义》《水浒传》《红楼梦》是我国古代长篇小说中的典型代表，被称为“四大古典名著”．某中学为了了解学生对四大古典名著的阅读情况，就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查.根据调查结果绘制成如所示的两个不完整的统计图，请结合图中信息解决下列问题：

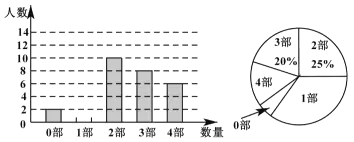
    (1) 本次调查一共抽取了______名学生；扇形统计图中“1部”所在扇形的圆心角为______度

    (2) 若该中学有1000名学生，请估计至少阅读3部四大古典名著的学生有多少名？

    (3) 没有读过四大名著的两名学生准备从四大古典名著中各自随机选择一部来阅读，则他们选中同一名著的概率为_________

    查看答案和解析>>

    科目：初中数学 来源： 题型：

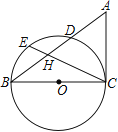
    【题目】如图，BC是⊙O的直径，AB交⊙O于点D，E为弧BD的中点，CE交AB于点H，AC＝AH

    (1) 求证：AC与⊙O相切

    (2) 若CH＝3EH，求sin∠ABC的值

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料：

    材料一：

    早在2011年9月25日，北京故宫博物院就开始尝试网络预售门票，2011年全年网络售票仅占1.68%.2012年至2014年，全年网络售票占比都在2%左右.2015年全年网络售票占17.33%，2016年全年网络售票占比增长至41.14%.2017年8月实现网络售票占比77%.2017年10月2日，首次实现全部网上售票.与此同时，网络购票也采用了“人性化”的服务方式，为没有线上支付能力的观众提供代客下单服务.实现全网络售票措施后，在北京故宫博物院的精细化管理下，观众可以更自主地安排自己的行程计划，获得更美好的文化空间和参观体验.

    材料二：

    以下是某同学根据网上搜集的数据制作的2013-2017年度中国国家博物馆参观人数及年增长率统计表.

    年度

    2013

    2014

    2015

    2016

    2017

    参观人数（人次）

    7 450 000

    7 630 000

    7 290 000

    7 550 000

    8 060 000

    年增长率（%）

    38.7

    2.4

    -4.5

    3.6

    6.8

    他还注意到了如下的一则新闻：2018年3月8日，中国国家博物馆官方微博发文，宣布取消纸质门票，观众持身份证预约即可参观. 国博正在建设智慧国家博物馆，同时馆方工作人员担心的是：“虽然有故宫免（纸质）票的经验在前，但对于国博来说这项工作仍有新的挑战.参观故宫需要观众网上付费购买门票，他遵守预约的程度是不一样的.但（国博）免费就有可能约了不来，挤占资源，所以难度其实不一样.” 尽管如此，国博仍将积极采取技术和服务升级，希望带给观众一个更完美的体验方式.

    根据以上信息解决下列问题：

    （1）补全以下两个统计图；

    （2）请你预估2018年中国国家博物馆的参观人数，并说明你的预估理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，在平面直角坐标系中，矩形OABC的边OA、OC分别在x轴的正半轴、y轴的正半轴上，且OA、OC（）的长是方程的两个根．

    （1）如图，求点A的坐标；

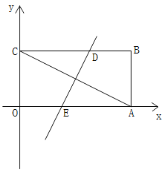
    （2）如图，将矩形OABC沿某条直线折叠，使点A与点C重合，折痕交CB于点D，交OA于点E．求直线DE的解析式；

    （3）在（2）的条件下，点P在直线DE上，在直线AC上是否存在点Q，使以点A、B、P、Q为顶点的四边形是平行四边形．若存在，请求出点Q坐标；若不存在，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点P、Q在数轴上表示的数分别是－8、4，点P以每秒2个单位的速度运动，点Q以每秒1个单位的速度运动．设点P、Q同时出发向右运动，运动时间为t秒．

    （1）若运动2秒时，则点P表示的数为_______，点P、Q之间的距离是______个单位；

    （2）求经过多少秒后，点P、Q重合？

    （3）试探究：经过多少秒后，点P、Q两点间的距离为6个单位．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，两个边长分别为a，b（a＞b）的正方形连在一起，三点C，B，F在同一直线上，反比例函数y=在第一象限的图象经过小正方形右下顶点E．若OB2﹣BE2=10，则k的值是（　　）

    A. 3 B. 4 C. 5 D. 4

    查看答案和解析>>

    同步练习册答案