
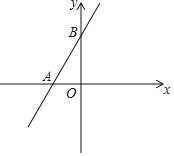
【题目】已知直线AB的函数表达式为y=![]() x+4,交x轴于点A,交y轴于点B,动点C从点A出发,以每秒2个单位长度的速度沿x轴正方向运动,设运动时间为t秒.
x+4,交x轴于点A,交y轴于点B,动点C从点A出发,以每秒2个单位长度的速度沿x轴正方向运动,设运动时间为t秒.
(1)求点A、B两点的坐标;
(2)当t为何值时,经过B、C两点的直线与直线AB关于y轴对称?并求出直线BC的函数关系式;
(3)在第(2)问的前提下,在直线AB上是否存在一点P,使得S△BCP=2S△ABC?如果存在,请求出此时点P的坐标;如果不存在,请说明理由.
【答案】(1)B(0,4),A(﹣3,0);(2)t=3秒,直线BC解析式为:y=﹣![]() x+4;(3)见解析.
x+4;(3)见解析.
【解析】
(1)令=0,则y=4可求出点B的坐标,令y=0,则0=![]() x+4可求得点A的坐标;
x+4可求得点A的坐标;
(2)先求出点A′的坐标,即点C的坐标,运用待定系数法可得直线BC的解析式;
(3)分两种情况:当点P在第三象限时,当点P在第一象限时分别求解即可.
(1)令=0,则y=4,
则点B(0,4),
令y=0,则0=![]() x+4,解得:x=﹣3,
x+4,解得:x=﹣3,
则点A(﹣3,0).
(2)点A关于y轴点对称点为A′(3,0),
所以当点C运动到A′(3,0)时,直线BC与直线AB关于y轴对称,则t=![]() =3秒.
=3秒.
设此时直线BC的解析式为:y=kx+b.
把点C(3,0)和点B(0,4)代入得:![]() ,
,
解得: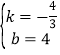 .
.
故直线BC解析式为:y=﹣![]() x+4.
x+4.
(3)存在,如图,当点P在第三象限时,S△BCP=2S△ABC,则S△ACP=S△ABC,
∴点P到x轴的距离等于点B到x轴的距离,
∴点P的纵坐标为﹣4,
把y=﹣4代入到y=![]() x+4中得:﹣4=
x+4中得:﹣4=![]() x+4,
x+4,
解得:x=﹣6,
则P(﹣6,﹣4);
当点P在第一象限时,S△BCP=2S△ABC,则S△ACP=3S△ABC,
∴点P到x轴的距离等于点B到x轴的距离,
∴点P的纵坐标为12,
把y=12代入到y=![]() x+4中得:12=
x+4中得:12=![]() x+4,
x+4,
解得:x=6,
则P'(6,12),
即:点P的坐标为(﹣6,﹣4)或(6,12).



 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
【题目】某商场第一次用11000元购进某款拼装机器人进行销售,很快销售一空,商家又用24000元第二次购进同款机器人,所购进数量是第一次的2倍,但单价贵了10元.
(1)求该商家第一次购进机器人多少个?
(2)若所有机器人都按相同的标价销售,要求全部销售完毕的利润率不低于20%(不考虑其它因素),那么每个机器人的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎,该打车方式的总费用由里程费和耗时费组成,其中里程费按x元/公里计算,耗时费按y元/分钟计算(总费用不足9元按9元计价).小明、小刚两人用该打车方式出行,按上述计价规则,其打车总费用、行驶里程数与打车时间如表:
时间(分钟) | 里程数(公里) | 车费(元) | |
小明 | 8 | 8 | 12 |
小刚 | 12 | 10 | 16 |
(1)求x,y的值;
(2)如果小华也用该打车方式,打车行驶了11公里,用了14分钟,那么小华的打车总费用为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过点A1(1,0)作x轴的垂线,交直线y=2x于点B1;点A2与点O关于直线A1B1对称;过点A2(2,0)作x轴的垂线,交直线y=2x于点B2;点A3与点O关于直线A2B2对称;过点A3(4,0)作x轴的垂线,交直线y=2x于点B3;…,按此规律作下去,则点Bn的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象经过点(﹣1,4),且与直线y=﹣ ![]() x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(﹣3,0).
x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(﹣3,0).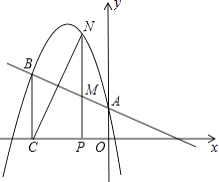
(1)求二次函数的表达式;
(2)点N是二次函数图象上一点(点N在AB上方),过N作NP⊥x轴,垂足为点P,交AB于点M,求MN的最大值;
(3)在(2)的条件下,点N在何位置时,BM与NC相互垂直平分?并求出所有满足条件的N点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC,ADEF的顶点A,D,C在坐标轴上,点F在AB 上,点B,E在函数 ![]() (
( ![]() )的图象上,若阴影部分的面积为12 -
)的图象上,若阴影部分的面积为12 - ![]() ,则点E的坐标是
,则点E的坐标是 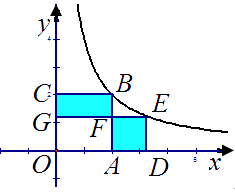
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一项工程,甲队单独做需40天完成,若乙队先做30天后,甲、乙两队一起合做20天恰好完成任务,请问:
(1)乙队单独做需要多少天才能完成任务?
(2)现将该工程分成两部分,甲队做其中一部分工程用了x天,乙队做另一部分工程用了y天,若x; y都是正整数,且甲队做的时间不到15天,乙队做的时间不到70天,那么两队实际各做了多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)探究新知:如图1,已知△ABC与△ABD的面积相等,试判断AB与CD的位置关系,并说明理由.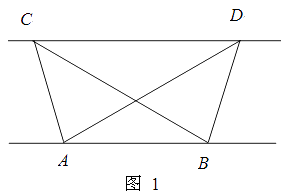
(2)结论应用:① 如图2,点M,N在反比例函数 ![]() (k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.试证明:MN∥EF.
(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.试证明:MN∥EF. 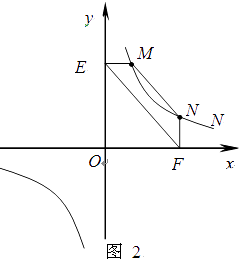
② 若①中的其他条件不变,只改变点M,N的位置如图3所示,请判断 MN与EF是否平行?请说明理由.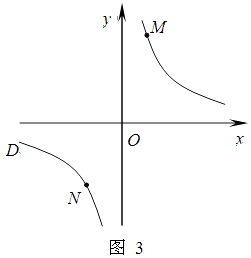
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+ ![]() x+1(a≠0)与x轴交于A,B两点,其中点B坐标为(2,0).
x+1(a≠0)与x轴交于A,B两点,其中点B坐标为(2,0).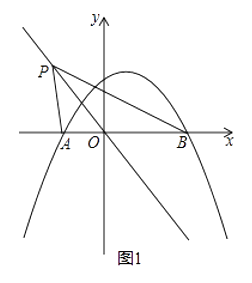
(1)求抛物线的解析式和点A的坐标;
(2)如图1,点P是直线y=﹣x上的动点,当直线OP平分∠APB时,求点P的坐标;
(3)如图2,在(2)的条件下,点C是直线BP上方的抛物线上的一个动点,过点C作y轴的平行线,交直线BP于点D,点E在直线BP上,连结CE,以CD为腰的等腰△CDE的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.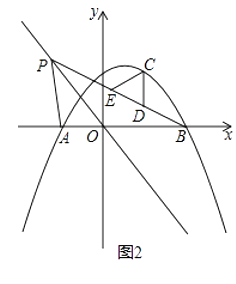
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com