
分析 (1)原式利用同底数幂的乘法、除法法则计算,合并即可得到结果;
(2)原式利用幂的乘方与积的乘方运算法则计算,即可得到结果;
(3)原式变形后,利用同底数幂的乘除法则计算即可得到结果;
(4)原式利用幂的乘方与积的乘方运算法则计算,合并即可得到结果;
(5)原式利用负指数幂,零指数幂法则计算即可得到结果.
解答 解:(1)原式=a6-a6=0;
(2)原式=-t3•t4•(-t)5=-t12;
(3)原式=-(p-q)4÷(p-q)3•(p-q)2=-(p-q)3;
(4)原式=-27a3+9a3=-18a3;
(5)原式=4-$\frac{1}{4}$-9÷1=4-$\frac{1}{4}$-9=-5$\frac{1}{4}$.
点评 此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:解答题
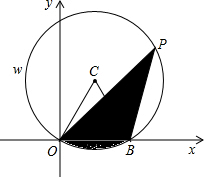 如图,在平面直角坐标系xOy中,⊙C经过点O,交x轴的正半轴于点B(2,0),P是$\widehat{OwB}$上的一个动点,且∠OPB=30°.设P点坐标为(m,n)
如图,在平面直角坐标系xOy中,⊙C经过点O,交x轴的正半轴于点B(2,0),P是$\widehat{OwB}$上的一个动点,且∠OPB=30°.设P点坐标为(m,n)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
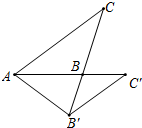 如图,△ABC中,∠ABC>90°,tan∠BAC=$\frac{3}{4}$,BC=4,将三角形绕着点A旋转,点C落在直线AB上的点C′处,点B落在点B′处.若C、B、B′恰好在一直线上,则AB的长为$\frac{6\sqrt{10}}{5}$.
如图,△ABC中,∠ABC>90°,tan∠BAC=$\frac{3}{4}$,BC=4,将三角形绕着点A旋转,点C落在直线AB上的点C′处,点B落在点B′处.若C、B、B′恰好在一直线上,则AB的长为$\frac{6\sqrt{10}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
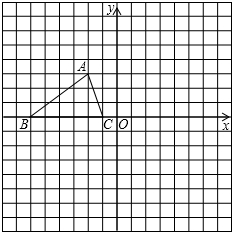 如图,已知△ABC的三个顶点的坐标分别为A(-2,3)B(-6,0),C(-1,0).
如图,已知△ABC的三个顶点的坐标分别为A(-2,3)B(-6,0),C(-1,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com