
【题目】已知![]() 是一段圆弧上的两点,有在直线
是一段圆弧上的两点,有在直线![]() 的同侧,分别过这两点作
的同侧,分别过这两点作![]() 的垂线,垂足为
的垂线,垂足为![]() ,
, ![]() 是
是![]() 上一动点,连结
上一动点,连结![]() ,且
,且![]() .
.
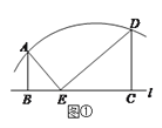
(1)如图①,如果![]() ,且
,且![]() ,求
,求![]() 的长.
的长.
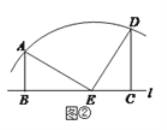
(2)(i)如图②,若点E恰为这段圆弧的圆心,则线段![]() 之间有怎样的等量关系?请写出你的结论并予以证明.
之间有怎样的等量关系?请写出你的结论并予以证明.
(ii)再探究:当![]() 分别在直线
分别在直线![]() 两侧且
两侧且![]() ,而其余条件不变时,线段
,而其余条件不变时,线段![]() 之间又有怎样的等量关系?请直接写出结论,不必证明.
之间又有怎样的等量关系?请直接写出结论,不必证明.
【答案】(1)![]() ;(2)(i)
;(2)(i)![]() ,证明见解析;(ii)当A、D分别在直线
,证明见解析;(ii)当A、D分别在直线![]() 两侧时,线段AB、BC、CD有如下等量关系:
两侧时,线段AB、BC、CD有如下等量关系: ![]() (
(![]() )或
)或![]() (
(![]() ).
).
【解析】解:(1)∵AB⊥![]() 于B,DC⊥
于B,DC⊥![]() 于C,
于C,
∴∠ABE=∠ECD=90°.
∵∠BEA+∠AED+∠CED=180°,且∠AED=90°,
∴∠CED=90°-∠BEA.
又∠BAE=90°-∠BEA,
∴∠BAE=∠CED.
∴Rt△ABE∽Rt△ECD.
(或:∵AB⊥![]() 于B,DC⊥
于B,DC⊥![]() 于C,∴AB∥DC.∴Rt△ABE∽Rt△ECD).
于C,∴AB∥DC.∴Rt△ABE∽Rt△ECD).
∴![]() .
.
∵![]() ,
, ![]() ,
,
∴![]() .
.
又![]() ,∴
,∴![]() .
.
在![]() 中,由勾股定理,得
中,由勾股定理,得
∴![]()
![]()
![]() .
.
(2)(i)猜想: ![]() .
.

证明:在Rt△ABE中,∵∠ABE=90°,
∴∠BAE=90°-∠AEB.
又∵∠AEB+∠AED+∠CED=180°,
且∠AED=90°,
∴∠CED=90°-∠AEB.
∴∠BAE=∠CED.
∵DC⊥BC于点C,∴∠ECD=90°.
由已知,有![]() .
.
于是在Rt△ABE和Rt△ECD中,
∵∠ABE=∠ECD=90°,∠BAE=∠CED, ![]() ,
,
∴Rt△ABE≌Rt△ECD.(AAS)
∴![]() .
.
∴![]() .即
.即![]() .
.
(ii)当A、D分别在直线![]() 两侧时,线段AB、BC、CD有如下等量关系:
两侧时,线段AB、BC、CD有如下等量关系:
![]() (
(![]() )或
)或![]() (
(![]() ).
).


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】在频率分布直方图中,以下说法错误的是( )
A.每个小长方形的面积等于频数
B.每个小长方形的面积等于频率
C.频率=频数÷数据总数
D.各个小长方形面积和等于1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一些相同的“○”按如图所示的规律依次摆放,观察每个“龟图”中的“○”的个数,若第n个“龟图”中有245个“○”,则n=( )

A. 14 B. 15 C. 16 D. 17
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线相交于点O,AE平分∠BAD交BC于E,若∠CAE=15°,则∠AEO=( )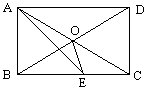
A.30°
B.25°
C.22.5°
D.20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD为正方形, E为CD边上的一点,连接AE,并以AE为对称轴,作与△ADE成轴对称的图形△AFE,延长EF(或FE)交直线BC于G。
(1)求证:DE+BG=EG;∠EAG=45°;
(2)AB=1,GF=m,FE=n,求m+n+mn的值;
(3)若AB=6,∠BAG=∠CEG,求GE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com