
����Ŀ����ͼ����֪��ABC�У�AB=10cm��AC=8cm��BC=6cm�������P��B������BA���A�����˶���ͬʱ��Q��A������AC���C�����˶������ǵ��ٶȾ�Ϊ2cm/s������PQ�����˶���ʱ��Ϊt����λ��s����0��t��4����
��1����tΪ��ֵʱ��PQ��BC��
��2�����AQP�����ΪS����λ��cm2������tΪ��ֵʱ��Sȡ�����ֵ����������ֵ��
��3���Ƿ����ijʱ��t��ʹ�߶�PQǡ�ðѡ�ABC�����ƽ�֣������ڣ������ʱt��ֵ���������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺������֪��BP=2t��AP=10��2t��AQ=2t��
��PQ��BC��
���APQ�ס�ABC��
�� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
t= ![]() ��
��
����tΪ ![]() sʱ��PQ��BC��
sʱ��PQ��BC��
��2��
�⣺��AB=10cm��AC=8cm��BC=6cm��
��AB2=AC2+BC2��
���C=90�㣬
��P��PD��AC��D��
��PD��BC��
���APD�ס�ABC��
�� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
PD= ![]() ��10��2t����
��10��2t����
��S= ![]() AQPD=
AQPD= ![]() 2t
2t ![]() ��10��2t��=��
��10��2t��=�� ![]() t2+6t=��
t2+6t=�� ![]() ��t��
��t�� ![]() ��2+7.5��
��2+7.5��
�ߩ� ![]() ��0���������£������ֵ��
��0���������£������ֵ��
��t= ![]() ��ʱ��S�����ֵ��7.5cm2��
��ʱ��S�����ֵ��7.5cm2��

��3��
�⣺�������ijʱ��t��ʹ�߶�PQǡ�ðѡ�ABC�����ƽ�֣�
��S��APQ= ![]() S��ABC
S��ABC
���� ![]() t2+6t=
t2+6t= ![]() ��
�� ![]() ��8��6
��8��6
t2��5t+10=0��
�ߡ�=52��4��1��10=��15��0��
��˷����⣬
��������ijʱ��t��ʹ�߶�PQǡ�ðѡ�ABC�����ƽ�֣�
����������1��֤��APQ�ס�ABC���Ƴ� ![]() =
= ![]() ������ó�
������ó� ![]() =
= ![]() ��������̵Ľ⼴�ɣ�2�������C=90�㣬��P��PD��AC��D��֤��APD�ס�ABC������ó�����
��������̵Ľ⼴�ɣ�2�������C=90�㣬��P��PD��AC��D��֤��APD�ס�ABC������ó����� ![]() =
= ![]() �����PD=
�����PD= ![]() ��10��2t�������������ε������ʽ������ɣ���3���������ijʱ��t��ʹ�߶�PQǡ�ðѡ�ABC�����ƽ�֣��ó����̩�
��10��2t�������������ε������ʽ������ɣ���3���������ijʱ��t��ʹ�߶�PQǡ�ðѡ�ABC�����ƽ�֣��ó����̩� ![]() t2+6t=
t2+6t= ![]() ��
�� ![]() ��8��6������˷����⣬���ɵó��𰸣�
��8��6������˷����⣬���ɵó��𰸣�
�����㾫����������Ĺؼ������������������ε����ʵ����֪ʶ�����ն�Ӧ����ȣ���Ӧ�߳ɱ��������������ν������������Σ��Լ������������ε��ж������⣬�˽����������ε��ж�����:���Ƕ�Ӧ��ȣ������������ƣ�ASA����ֱ�������α�б���ϵĸ߷ֳɵ�����ֱ�������κ�ԭ���������ƣ� ���߶�Ӧ�ɱ����Ҽн���ȣ������������ƣ�SAS�������߶�Ӧ�ɱ����������������ƣ�SSS����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����x1 �� x2��x1��x2���Ƿ��̣�x��a����x��b��=1��a��b��������������ʵ��x1 �� x2 �� a��b�Ĵ�С��ϵΪ�� ��
A.x1��x2��a��b
B.x1��a��x2��b
C.x1��a��b��x2
D.a��x1��b��x2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ij���������ֲ������A��B����Ʒ�ֵ�������ۣ���֪A�ֱ�B��ÿ���2Ԫ����1��A�������2��B�����繲��20Ԫ��
��1����A��B��������ÿ��ֱ��Ƕ���Ԫ��
��2��Ϊ������ֲ��ijũ��������A��B�������繲360�꣬��A����������������B��������һ�룬�����������ʡ�Ĺ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��������ִ�ͬʱ�Ӹۿ�A���������ִ���ÿСʱ30������ٶ����ű�ƫ��60��ķ����У����ִ���ÿСʱ15������ٶ��������������н���1Сʱ�״��ӵ�����Ҫ���Ҵ���ϣ����Ǽ״��ı����н����ٶȣ����Ŷ��Ϸ����У������С��C�����Ҵ������������Ҵ����ٶȺͺ��ֲ��䣬��
��1���ۿ�A��С��C֮��ľ��룻
��2�����ִ��������ٶȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����OAC�͡�BAD���ǵ���ֱ�������Σ���ACO=��ADB=90�㣬����������y= ![]() �ڵ�һ����ͼ����B����OA2��AB2=12����k��ֵΪ ��
�ڵ�һ����ͼ����B����OA2��AB2=12����k��ֵΪ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD �У�AE ƽ�֡�BAD����BC ��E��DE��AE�����н��ۣ���DEƽ�֡�ADC����E ��BC ���е㣻��AD=2CD�����ı���ADCE ��������ABE���������3��1��������ȷ�Ľ��۵ĸ����У� ��
A.4
B.3
C.2
D.1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ƽ��ֱ������ϵ�У�������y= ![]() ��x �����������ֱ�ΪA����3��0����B��1��0������y��Ľ���ΪD���Գ����������߽��ڵ�C����x�Ḻ���ύ�ڵ�H.
��x �����������ֱ�ΪA����3��0����B��1��0������y��Ľ���ΪD���Գ����������߽��ڵ�C����x�Ḻ���ύ�ڵ�H.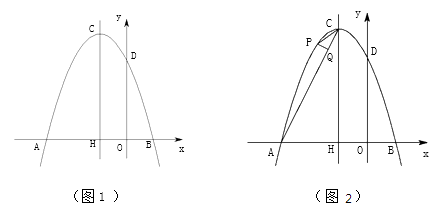
��1���������ߵı���ʽ��
��2����E��F �ֱ��������߶Գ���CH �ϵ��������㣨��E �ڵ�F �Ϸ�������EF=1����ʹ�ı���BDEF ���ܳ���Сʱ�ĵ�E��F ���꼰��Сֵ��
��3����ͼ2����P Ϊ�Գ�����࣬x ���Ϸ����������ϵĵ㣬PQ��AC ��AC �ڵ�Q���Ƿ���������ĵ�P ʹ��PCQ���ACH ���ƣ��������������P �����꣬����������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2+��k��5��x+1��k=0������kΪ������
��1����֤������kΪ��ֵ�������������������ʵ������
��2����֪����y=x2+��k��5��x+1��k��ͼ�����������ޣ���k��ȡֵ��Χ��
��3����ԭ���̵�һ��������3����һ����С��3����k���������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��P��AB������AB��һ���㣬����P��PM��AB��AB�ڵ�M������MB������P��PN��MB�ڵ�N����֪AB=6cm����A��P�����ľ���Ϊxcm��P��N�����ľ���Ϊycm��������P���A���B�غ�ʱ��y��ֵΪ0�� 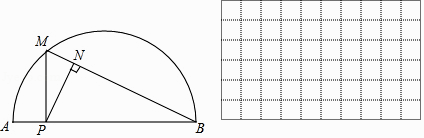
С������ѧϰ�����ľ��飬�Ժ���y���Ա���x�ı仯���仯�Ĺ��ɽ�����̽����
������С����̽�����̣��벹��������
��1��ͨ��ȡ�㡢��ͼ���������õ���x��y�ļ���ֵ�����±���
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 0 | 2.0 | 2.3 | 2.1 | 0.9 | 0 |
��˵������ȫ����ʱ�����ֵ����һλС����
��2������ƽ��ֱ������ϵ������Բ�ȫ��ı��и��Զ�ӦֵΪ����ĵ㣬�����ú�����ͼ�� 
��3����ϻ����ĺ���ͼ������⣺����PANΪ����������ʱ��AP�ij���ԼΪcm��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com