
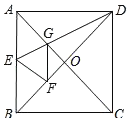
【题目】如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后,折痕DF分别交AB、AC于点E、G,连解FG,下列结论:(1)∠AGD=112.5°;(2)E为AB中点;(3)S△AGD=S△OCD;(4)正边形AEFG是菱形;(5)BE=2OG,其中正确结论的个是( )
A.2B.3C.4D.5
【答案】B
【解析】
利用翻折不变性可知:AG=GF,AE=EF,∠ADG=∠GDF=22.5°,再通过角度计算证明AE=AG,即可得到答案,具体见详解.
因为∠GAD=∠ADO=45°,由折叠可知:∠ADG=∠ODG=22.5°.
(1)∠AGD=180°﹣45°﹣22.5°=112.5°,故(1)正确;
(2)设OG=1,则AG=GF=![]() ,
,
又∠BAG=45°,∠AGE=67.5°,∴∠AEG=67.5°,
∴AE=AG=![]() ,则AC=2AO=2(
,则AC=2AO=2(![]() +1),
+1),
∴AB=![]() =2+
=2+![]() ,
,
∴AE≠EB,故(2)错误;
(3)由折叠可知:AG=FG,在直角三角形GOF中,
斜边GF>直角边OG,故AG>OG,两三角形的高相同,
则S△AGD>S△OGD,故(3)错误;
(4)中,AE=EF=FG=AG,故(4)正确;
(5)∵GF=EF,
∴BE=![]() EF=
EF=![]() GF=
GF=![]()
![]() OG=2OG,
OG=2OG,
∴BE=2OG,故(5)正确.
故选:B.


科目:初中数学 来源: 题型:
【题目】某文具店,甲种笔记本标价每本8元,乙种笔记本标价每本5元.今天,甲、乙两种笔记本合计卖了100本,共卖了695元!
(1)两种笔记本各销售了多少?
(2)所得销售款可能是660元吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:以直线AB上一点O为端点作射线OM、ON,将一个直角三角形的直角顶点放在O处(∠COD=90°).
(1)如图1,直角三角板COD的边OD放在射线OB上,OM平分∠AOC,ON和OB重合,则∠MON=_°;
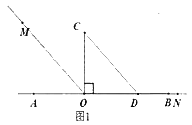
(2)直角三角板COD绕点O旋转到如图2的位置,OM平分∠AOC,ON平分∠BOD,求∠MON的度数。
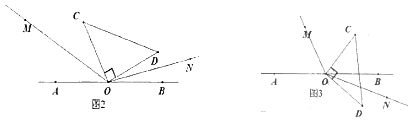
(3)直角三角板COD绕点O旋转到如图3的位置,OM平分∠ AOC ,ON平分∠BOD,猜想∠MON的度数,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车行驶时的耗油量为0.1升/千米,如图是油箱剩余油量![]() (升)关于加满油后已行驶的路程
(升)关于加满油后已行驶的路程![]() (千米)的函数图象.
(千米)的函数图象.

(1)根据图象,直接写出汽车行驶400千米时,油箱内的剩余油量,并计算加满油时油箱的油量;
(2)求![]() 关于
关于![]() 的函数关系式,并计算该汽车在剩余油量5升时,已行驶的路程.
的函数关系式,并计算该汽车在剩余油量5升时,已行驶的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
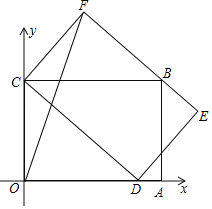
【题目】如图,矩形OABC的边OC在y轴上,边OA在x轴上,C点坐标为(0,3),点D是线段OA的一个动点,连接CD,以CD为边作矩形CDEF,使边EF过点B,已知所作矩形CDEF的面积为12,连接OF,则在点D的运动过程中,线段OF的最大值为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在数轴上有A 、B、C三个点,点A表示的数是-4,点B表示的数是-2,点C表示的数是2.
(1)在数轴上把A 、B、C三点表示出来,并比较各数的大小(用“<”连接);
(2)如何移动点B,使它到点A和点C的距离相等 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】再读教材:
宽与长的比是 ![]() (约为0.618)的矩形叫做黄金矩形,黄金矩形给我们以协调,匀称的美感.世界各国许多著名的建筑.为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为2的矩形纸片折叠黄金矩形.(提示; MN=2)
(约为0.618)的矩形叫做黄金矩形,黄金矩形给我们以协调,匀称的美感.世界各国许多著名的建筑.为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为2的矩形纸片折叠黄金矩形.(提示; MN=2)
第一步,在矩形纸片一端.利用图①的方法折出一个正方形,然后把纸片展平.
第二步,如图②.把这个正方形折成两个相等的矩形,再把纸片展平.
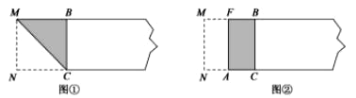
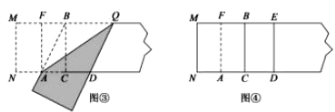
第三步,折出内侧矩形的对角线 AB,并把 AB折到图③中所示的AD处,
第四步,展平纸片,按照所得的点D折出 DE,使 DE⊥ND,则图④中就会出现黄金矩形,
问题解决:
(1)图③中AB=________(保留根号);
(2)如图③,判断四边形 BADQ的形状,并说明理由;
(3)请写出图④中所有的黄金矩形,并选择其中一个说明理由.
(4)结合图④.请在矩形 BCDE中添加一条线段,设计一个新的黄金矩形,用字母表示出来,并写出它的长和宽.
查看答案和解析>>
科目:初中数学 来源: 题型:
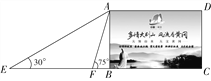
【题目】在黄冈长江大桥的东端一处空地上,有一块矩形的标语牌ABCD(如图4所示).已知标语牌的高AB=5 m,在地面的点E处,测得标语牌点A的仰角为30°,在地面的点F处,测得标语牌点A的仰角为75°,且点E,F,B,C在同一直线上.求点E与点F之间的距离(计算结果精确到0.1 m,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73).
≈1.73).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com