
【题目】如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
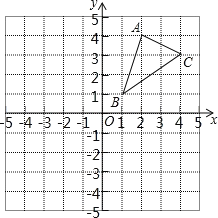
(1)请画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
(2)请画出△ABC绕点B逆时针旋转90后的△A2BC2;
(3)求出(2)中C点旋转到C2点所经过的路径长(结果保留根号和π).
(4)在x轴上有一点P,PA+PB的值最小,请直接写出点P的坐标
【答案】(1)根A1(2,4),B1(1,1),C1(4,3)(2)图形见解析(3) ![]() (4)(1.2,0)
(4)(1.2,0)
【解析】试题分析:(1)利用关于x轴对称点的横坐标相等,纵坐标互为相反数可先找出点A1、B1、C1的坐标,然后画出图形即可;
(2)利用旋转的性质可确定出点A2、C2的坐标;
(3)先求出BC的长,然后利用弧长公式进行计算即可;
(4)连接A1B,与x轴相交于点P,则此时PA+PB的值最小.利用待定系数法求出直线A1B的解析式,然后求出与x轴的交点即可.
试题解析:
(1)根据关于x轴对称点的坐标特点可知:A1(2,4),B1(1,1),C1(4,3),
如下图:连接A1、B1、C1即可得到△A1B1C1.
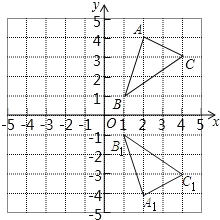
(2)如图:
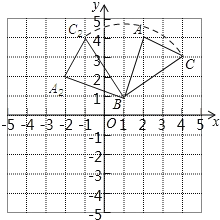
(3)由两点间的距离公式可知:BC=![]() ,
,
∴点C旋转到C2点的路径长=![]()
(4)连接A1B,与x轴相交于点P,则此时PA+PB的值最小.
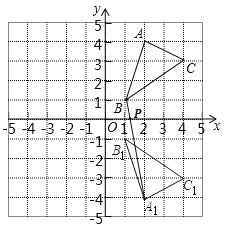
设直线A1B的解析式为y=kx+b,
则![]() ,
,
解得![]() ,
,
∴直线A1B的解析式为y=-5x+6,
令y=0,则-5x+6=0,
x=1.2,
所以点P的坐标为(1.2,0).


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
【题目】已知,如图,点A,B,C,D在一条直线上,填写下列空格:
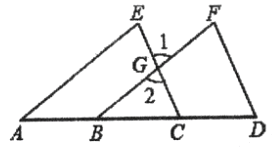
∵AE∥BF(已知)
∴∠E=∠1(______________________)
∵∠E=∠F(已知〉
∴∠_____=∠F(________________)
∴________∥_________(________________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
某商店经销《超能陆战队》超萌“小白”(图1)玩具,“小白”玩具每个进价60元.为进行促销,商店制定如下“优惠”方案:如果一次销售数量不超过10个,则销售单价为100元/个;如果一次销售数量超过10个,每增加一个,所有“小白”玩具销售单价降低1元/个,但单价不得低于80元/个.一次销售“小白”玩具的单价y(元/个)与销售数量x(个)之间的函数关系如图2所示.

(1)求m的值并解释射线BC所表示的实际意义;
(2)写出该店当一次销售x个时,所获利润w(元)与x(个)之间的函数关系式;
(3)店长经过一段时间的销售发现:即并不是销量越大利润越大(比如,卖25个赚的钱反而比卖30个赚的钱多).为了不出现这种现象,在其他条件不变的情况下,店长应把原来的最低单价80(元/个)至少提高到多少元/个?
查看答案和解析>>
科目:初中数学 来源: 题型:
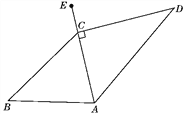
【题目】为倡导“低碳生活”,人们常选择以自行车作为代步工具,如图是一辆自行车的部分几何示意图,其中车架档AC与CD的长分别为45 cm和60 cm,且它们互相垂直,座杆CE的长为20 cm,点A,C,E在同一条直线上,且∠CAB=75°.(参考数据:sin 75°≈0.966,cos 75°≈0.259,tan 75°≈3.732)
(1)求车架档AD的长;
(2)求车座点E到车架档AB的距离(结果精确到1 cm).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,都是由边长为1的正方体叠成的立体图形,例如第(1)个图形由1个正方体叠成,第(2)个图形由4个正方体叠成,第(3)个图形由10个正方体叠成,依次规律,第(8)个图形有多少个正方体叠成( )

A.120个B.121个C.122个D.123个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为![]() 的大正方形,两块是边长都为
的大正方形,两块是边长都为![]() 的小正方形,五块是长为
的小正方形,五块是长为![]() 、宽为
、宽为![]() 的全等小矩形,且
的全等小矩形,且![]() >
> ![]() .(以上长度单位:cm)
.(以上长度单位:cm)
(1)观察图形,可以发现代数式![]() 可以因式分解为 ;
可以因式分解为 ;
(2)若每块小矩形的面积为10![]() ,四个正方形的面积和为58
,四个正方形的面积和为58![]() ,试求图中所有裁剪线(虚线部分)长之和.
,试求图中所有裁剪线(虚线部分)长之和.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是等腰直角△ABC外一点,把BP绕点B顺时针旋转90°到BP′,已知∠AP′B=135°,P′A∶P′C=1∶3,则P′A∶PB=( )

A. 1∶![]() B. 1∶2 C.
B. 1∶2 C. ![]() ∶2 D. 1∶
∶2 D. 1∶![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
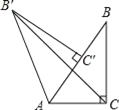
【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AB=2.Rt△AB′C′可以看作是由Rt△ABC绕A点逆时针方向旋转60°得到的,求线段 B′C的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
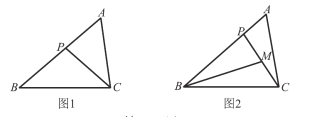
【题目】在△ABC中,P为边AB上一点.
(1)如图l,若∠ACP=∠B,求证:AC2 =AP·AB;
(2)若M为CP的中点,AC=2,如图2,若∠PBM=∠ACP,AB=3,求BP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com