
����Ŀ���ڼס������������ĺ����У��ֱ�װ�г���ɫ��������ȫ��ͬ��С�����У�����װ��2������1�������Һ���װ��2������1������
��1��������ҡ�Ⱥ����ȡ��һ��С����С���ǰ�ɫ�ĸ��ʣ�
��2��С����ͬ���̶�������������ҡ�Ⱥ��������һ��С������ɫ��ͬ����С����ʤ������ɫ��ͬ����ͬ����ʤ�������б�������״ͼ�ķ���˵��˭Ӯ�Ŀ����Դ�
���𰸡���1��![]() ����2��ͬ����ʤ��ʤ�Ŀ����Դ�����
����2��ͬ����ʤ��ʤ�Ŀ����Դ�����
��������
��1���ɸ��ʹ�ʽ���ɵó��𰸣�
��2�����б���֪������9�ֵȿ��ܽ����������ɫ����ͬ�Ľ����4�֣���ɫ��ͬ�Ľ����5�֣�P����ɫ����ͬ����![]() ��P����ɫ��ͬ����
��P����ɫ��ͬ����![]() �����ɵó��𰸣�
�����ɵó��𰸣�
�⣺��1������3�ֵȿ��ܽ��������������Ľ����2��
��P����������![]()
��2���������⣬�б����£�
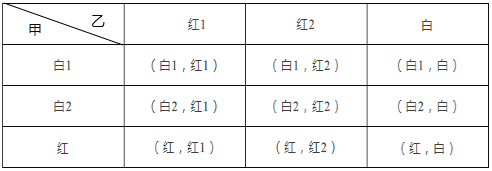
���ϱ���֪������9�ֵȿ��ܽ����������ɫ����ͬ�Ľ����5�֣���ɫ��ͬ�Ľ����4�֣�
��P����ɫ����ͬ����![]() ��P����ɫ��ͬ����
��P����ɫ��ͬ����![]() ����
����![]() ��
��![]() ��
��
��ͬ����ʤ��ʤ�Ŀ����Դ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һֻ�����Ĵ����У�װ��2�������1��������Щ�����ɫ�ⶼ��ͬ��
��1��С����Ϊ�����Ⱥ������������һ�����ǰ�����Ǻ����ǵȿ��ܵģ���ͬ������˵����Ϊʲô��
��2�����Ⱥ����һ��������������ͨ���б�����״ͼ����������ǰ���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Rt��ABC�У����ǹ涨��һ����ǵĶԱ���б�ߵı�ֵ��Ϊ�����ǵ�����ֵ��
���磺Rt��ABC�У���C��90������A�ĶԱ�BC��б��AB�ı�ֵ����![]() ���ǡ�A������ֵ�����������������������������ֵ�ٲ鿨���������������£�
���ǡ�A������ֵ�����������������������������ֵ�ٲ鿨���������������£�
��ͼ����OA��1����OΪԲ�ģ��ֱ���0.05��0.1��0.15��0.2������0.9��0.95��Ϊ�뾶����Բ������OAΪֱ������M���������������ֵ�ٲ鿨�����Զ�����Ӧ������ҵĽ���ֵ�����磺60��������ֵԼ��0.85��0.88֮��ȡֵ��45��������ֵԼ��0.70��0.72֮��ȡֵ�����нǶ�������ֵ��ӽ�0.94���ǣ�������
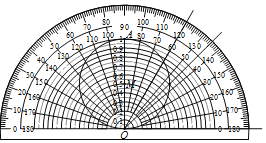
A.30��B.50��C.40��D.70��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �У�
��![]() ,��
,��![]() ������
������![]() ��һ���㣬��
��һ���㣬��![]() Ϊ�����Ҳ����ȱ�
Ϊ�����Ҳ����ȱ�![]() ����
����![]() ������
��λ�����![]() ��λ�ñ仯���仯.
��λ�ñ仯���仯.
��1����ͼ1������![]() ������
������![]() �ڲ������ʱ������
�ڲ������ʱ������![]() ��
��![]() ��
��![]() ��������ϵ�� ��
��������ϵ�� ��![]() ��
��![]() ��λ�ù�ϵ�� ��
��λ�ù�ϵ�� ��
��2������![]() ������
������![]() �ⲿʱ��(1)�еĽ����Ƿ�������������������֤��������������
�ⲿʱ��(1)�еĽ����Ƿ�������������������֤��������������
��˵������(ѡ��ͼ2��ͼ3�е�һ���������֤����˵��).
(3) ��ͼ4������![]() ���߶�
���߶�![]() ���ӳ�����ʱ������
���ӳ�����ʱ������![]() ����
����![]() ,
,![]() ,���ı���
,���ı���![]() �����.
�����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУѡѧ����������ϯ����Ҫ�Ӽװ��2������1��Ů����������A��B��ʾ��Ů����a��ʾ�����Ұ��1������1��Ů����������C��ʾ��Ů����b��ʾ����5�������ѡ��2��ͬѧ��
��1������״ͼ���б����г����п������Σ�
��2����2��ͬѧ���Բ�ͬ�༶�ĸ��ʣ�
��3����2��ͬѧǡ��1��1Ů�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2+![]() x+c��x����A��B���㣬��y���ڵ�C��ֱ��y����
x+c��x����A��B���㣬��y���ڵ�C��ֱ��y����![]() +2������A��C��
+2������A��C��
��1���������ߵĽ���ʽ��
��2����P���������ڵ�һ�����ڵ�ͼ���ϣ�����P��x��Ĵ��ߣ�����ΪD����ֱ��AC�ڵ�E������PC�����P�ĺ�����Ϊm��
�ٵ���PCE�ǵ���������ʱ����m��ֵ��
�ڹ���C��ֱ��PD�Ĵ��ߣ�����ΪF����F����ֱ��PC�ĶԳƵ�ΪF��������F��������������ʱ����ֱ��д����P�����꣮
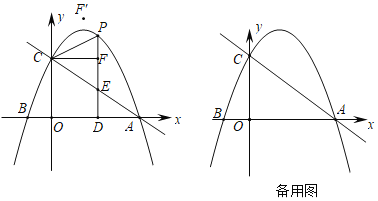
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y1=��x+4��y2=![]() x+b����˫����y=
x+b����˫����y=![]() ���ڵ�A��1��m����������ֱ�߷ֱ���x�ύ��B��C���㣮
���ڵ�A��1��m����������ֱ�߷ֱ���x�ύ��B��C���㣮
��1����y��x֮��ĺ�����ϵʽ��
��2��ֱ��д����x��0ʱ������ʽ![]() x+b��
x+b��![]() �Ľ⼯��
�Ľ⼯��
��3������P��x���ϣ�����AP����ABC������ֳ�1��3�����֣����ʱ��P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
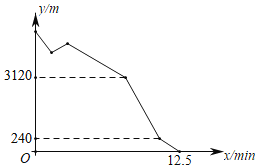
����Ŀ��10���ڼ䣬������ף���й�����70���������������������ƹ���չʾ�������İ�������ʵ�׳��֮������ĩ��С����С����Լһ������ȥ���ƹ��㣮��֪С���ҡ����վ��С����˳�ηֲ���ͬһ����ֱ�Ĺ�·�ϣ�С����С�������Ը��Ե��ٶȲ��е����վ��С������3���Ӻ�С���Ӽ�����������������ӣ�С������û�������������ͷ��ԭ�ٵ�![]() ���ؼ���ȡ��������ڼ���ȡͣ��5���ӣ�����ʱ����������������ǰס���վ�����ձ�С���絽2���ӣ���ͼ������֮��ľ�����С������ʱ��֮��Ĺ�ϵ����С���������վ�ľ����С���������վ�ľ�����_____�ף�
���ؼ���ȡ��������ڼ���ȡͣ��5���ӣ�����ʱ����������������ǰס���վ�����ձ�С���絽2���ӣ���ͼ������֮��ľ�����С������ʱ��֮��Ĺ�ϵ����С���������վ�ľ����С���������վ�ľ�����_____�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����֪������![]() ��
��![]() �ύ��
�ύ��![]() ��
��![]() ���㣬��
���㣬��![]() �ύ�ڵ�
�ύ�ڵ�![]() .
.
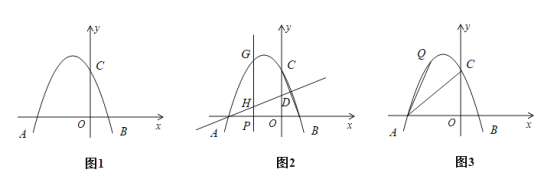
(1)�������ߵĽ���ʽ.
(2)��ͼ2��ֱ��![]() ��
��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��![]() ����
����![]() ����һ�����㣬����
����һ�����㣬����![]() ��
��![]() �ᣬ�������߽��ڵ�
�ᣬ�������߽��ڵ�![]() ����ֱ��
����ֱ��![]() ���ڵ�
���ڵ�![]() ������
������![]() ��
��![]() ��
��![]() ��
��![]() �ĸ�����ɵ��ı�����ƽ���ı���ʱ�����ʱ
�ĸ�����ɵ��ı�����ƽ���ı���ʱ�����ʱ![]() ������.
������.
(3)��ͼ3������![]() ��
��![]() ��
��![]() ������������һ�����㣬����
������������һ�����㣬����![]() ����
����![]() ʱ����
ʱ����![]() �������.
�������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com