
【题目】如图,在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,
,![]() 交于点
交于点![]() ,连接
,连接![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() 平分
平分![]() ;④
;④![]() 平分
平分![]() ,其中正确的序号是__________.
,其中正确的序号是__________.
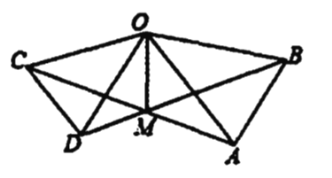
【答案】①②④
【解析】
由SAS证明△AOC≌△BOD得出∠OCA=∠ODB,AC=BD,①正确;
由全等三角形的性质得出∠OAC=∠OBD,由三角形的外角性质得:∠AMB+∠OAC=∠AOB+∠OBD,得出∠AMB=∠AOB=40°,②正确;
作OG⊥MC于G,OH⊥MB于H,如图所示:则∠OGC=∠OHD=90°,由AAS证明△OCG≌△ODH(AAS),得出OG=OH,由角平分线的判定方法得出MO平分∠BMC,④正确;
先假设OM平分∠AOD,推出OA=OC与条件中![]() 相矛盾,推出③错误.
相矛盾,推出③错误.
解:∵∠AOB=∠COD=40![]() ,
,
∴∠AOB+∠AOD=∠COD+∠AOD,
即∠AOC=∠BOD,
在△AOC和△BOD中,
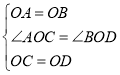 ,
,
∴△AOC![]() △BOD,
△BOD,
∴∠OCA=∠ODB,AC=BD,①正确;
∵△AOC![]() △BOD
△BOD
∴∠OAC=∠OBD,
由三角形的外角性质得:∠AMB+∠OAC=∠AOB+∠OBD,
∴∠AMB=∠AOB=40![]() ,
,
∴∠CMD=∠AMB=40![]() ,②正确;
,②正确;
作OG⊥MC于G,OH⊥MB于H,如图2所示:
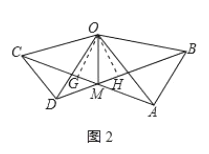
则∠OGC=∠OHD=90![]() ,
,
在△OCG和△ODH中,
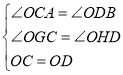 ,
,
∴△OCG![]() △ODH,
△ODH,
∴OG=OH,
∵OG⊥MC,OH⊥MB
∴MO平分∠BMC,④正确;
∵∠AOB=∠COD,
假设OM平分∠AOD,
∵OM平分∠AOD,
∴∠AOM=∠DOM,
∵△AOC≌△BOD,
∴∠COM=∠BOM,
∵MO平分∠BMC,
∴∠CMO=∠BMO,
在△COM和△BOM中,
∴△COM≌△BOM(ASA),
∴OB=OC,
∵OA=OB,
∴OA=OC,
与OA>OC矛盾,
故假设不成立,OM不平分∠AOD
∴③错误;
故答案为:①②④


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】随着景德镇市高铁的开通,给市民出行带来了极大的方便。据了解,景德镇与上海相距大约560km,高铁开通后,比此前开私家车去上海少用2小时20分,高铁的平均速度是私家车平均速度的1.5倍。
(1)求了从景德镇去上海的高铁和私家车的平均速度;
(2)一张景德镇至上海的高铁票价为212元,如果开私家车(六座)的话,从景德镇至上海过路费是240元,车子和油的损耗每千米0.8元。那么开私家车至少要几人一同去才会比坐高铁合算
查看答案和解析>>
科目:初中数学 来源: 题型:
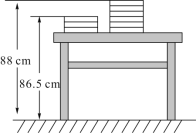
【题目】新学期开学,两摞规格相同准备发放的数学课本整齐地叠放在讲台上,请根据图中所给的数据信息,解答下列问题:
(1)一本数学课本的高度是多少厘米?
(2)讲台的高度是多少厘米?
(3)请写出整齐叠放在桌面上的x本数学课本距离地面的高度的代数式(用含有x的代数式表示);
(4)若桌面上有56本同样的数学课本,整齐叠放成一摞,从中取走18本后,求余下的数学课本距离地面的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点![]() 和点
和点![]() 是线段
是线段![]() 的两个端点,线段
的两个端点,线段![]() ,点
,点![]() 是点
是点![]() 和点
和点![]() 的对称中心,点
的对称中心,点![]() 是点
是点![]() 和点
和点![]() 的对称中心,以此类推,(图中未画出)点
的对称中心,以此类推,(图中未画出)点![]() 是点
是点![]() 和点
和点![]() 的对称中心.(
的对称中心.(![]() 为正整数)
为正整数)
![]()
(1)填空:线段![]() ____________ ;线段
____________ ;线段![]() _____________ (用含
_____________ (用含![]() 的最简代数式表示)
的最简代数式表示)
(2)试写出线段![]() 的长度(用含
的长度(用含![]() 和
和![]() 的代数式表示,无需说明理由)
的代数式表示,无需说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车制造厂开发了一款新式自行车,计划6月份生产安装600辆,由于抽调不出足够的熟练工来完成新式自行车的安装,工厂决定招聘一些新工人:他们经过培训后也能独立进行安装.调研部门发现:1名热练工和2名新工人每日可安装8辆自行车;2名熟练工和3名新工人每日可安装14辆自行车.
(1)每名熟练工和新工人每日分别可以安装多少辆自行车?
(2)如果工厂招聘n名新工人(0<n<10).使得招聘的新工人和抽调熟练工刚好能完成6月份(30天) 的安装任务,那么工厂有哪几种新工人的招聘方案?
(3)该自行车关于轮胎的使用有以下说明:本轮胎如安装在前轮,安全行使路程为11千公里;如安装在后轮,安全行使路程为9千公里.请问一对轮胎能行使的最长路程是多少千公里?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆慢车从甲地匀速行驶至乙地,一辆快车同时从乙地出发匀速行驶至甲地,两车之间的距离y(千米)与行驶时间x(小时)的对应关系如图所示,下列叙述正确的是( )
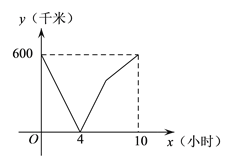
A. 甲乙两地相距1200千米
B. 快车的速度是80千米∕小时
C. 慢车的速度是60千米∕小时
D. 快车到达甲地时,慢车距离乙地100千米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校八、九两个年级各有学生180人,为了解这两个年级学生的体质健康情况,进行了抽样调查,过程如下,请补充完整.
收集数据
从八、九两个年级各随机抽取![]() 名学生,进行了体质健康测试,测试成绩(百分制)如下:
名学生,进行了体质健康测试,测试成绩(百分制)如下:
八年级 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
九年级 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
整理、描述数据
按如下分数段整理、描述这两组样本数据:
|
|
|
|
|
| |
八年级 | 0 | 0 | 1 | 11 | 1 | |
九年级 | 1 | 0 | 0 | 7 |
(说明:成绩![]() 分及以上为体质健康优秀,
分及以上为体质健康优秀,![]() ~
~![]() 分为体质健康良好,
分为体质健康良好,![]() ~
~![]() 分为体质健康合格,
分为体质健康合格,![]() 分以下为体质健康不合格)
分以下为体质健康不合格)
分析数据
两组样本数据的平均数、中位数、众数、方差如下表所示:
年级 | 平均数 | 中位数 | 众数 | 方差 |
八年级 |
|
|
| 33.6 |
九年级 |
|
| 52.1 |
请将以上两个表格补充完整;
得出结论
(1)估计九年级体质健康优秀的学生人数为__________;
(2)可以推断出_______年级学生的体质健康情况更好一些,理由为_________________.(至少从两个不同的角度说明推断的合理性).
查看答案和解析>>
科目:初中数学 来源: 题型:
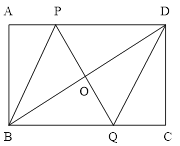
【题目】如图,在矩形ABCD中,P是AD上一动点,O为BD的中点,连接PO并延长,交BC于点Q.
(1) 求证:四边形PBQD是平行四边形
(2) 若AD=6cm,AB=4cm, 点P从点A出发,以1cm/s的速度向点D运动(不与点D重合),设点P运动时间为t s , 请用含t的代数式表示PD的长,并求出当t为何值时,四边形PBQD是菱形。并求出此时菱形的周长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人分别从相距100km的A、B两地同时出发相向而行,并以各自的速度匀速行驶.甲出发2h后到达B地立即按原路返回,返回时速度提高了30km/h,回到A地后在A地休息等乙,乙在出发5h后到达A地.(友情提醒:可以借助用线段图分析题目)
(1)乙的速度是_______![]() ,甲从A地到B地的速度是_______
,甲从A地到B地的速度是_______![]() ,甲在出发_______小时到达A地.
,甲在出发_______小时到达A地.
(2)出发多长时间两人首次相遇?
(3)出发多长时间时,两人相距30千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com