
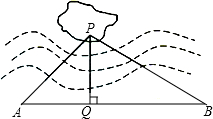
 如图,某湖中有一孤立的小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PQ通往小岛,某同学在观光道AB上测得如下数据:AB=100米,∠PAB=45°,∠PBA=30.请求出小桥PQ的长.(
如图,某湖中有一孤立的小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PQ通往小岛,某同学在观光道AB上测得如下数据:AB=100米,∠PAB=45°,∠PBA=30.请求出小桥PQ的长.(| 2 |
| 3 |
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
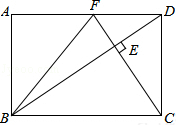 在矩形ABCD中,DC=
在矩形ABCD中,DC=| 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在Rt△ABC中,∠C=90°,以边AC为直径作⊙O,与斜边AB交于点M,点N是边BC的中点,连接MN.
如图,在Rt△ABC中,∠C=90°,以边AC为直径作⊙O,与斜边AB交于点M,点N是边BC的中点,连接MN. | 3 |
| 2 |
| 3 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
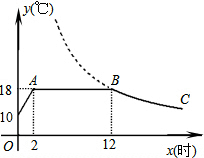 我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培蔬菜.图中是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=
我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培蔬菜.图中是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
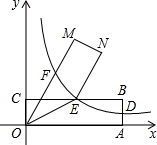 如图,点A、C分别在x轴、y轴的正半轴上移动,过点O、A、C作矩形OABC,OA=a,OC=c,在移动过程中,双曲线y=
如图,点A、C分别在x轴、y轴的正半轴上移动,过点O、A、C作矩形OABC,OA=a,OC=c,在移动过程中,双曲线y=| k |
| x |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com