
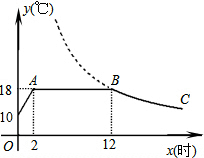
 我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培蔬菜.图中是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=
我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培蔬菜.图中是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=| k |
| x |
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
| 班级 | 平均数 | 方差 | 中位数 |
| 九(1)班 | 168 | 168 | |
| 九(2)班 | 3.8 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 抛物线y=x2-kx-3与x轴交于点A,B,与y轴交于点C,其中点B的坐标为(1+k,0).
抛物线y=x2-kx-3与x轴交于点A,B,与y轴交于点C,其中点B的坐标为(1+k,0).查看答案和解析>>
科目:初中数学 来源: 题型:
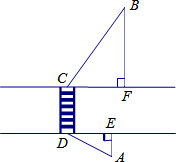 如图,从超市A到马路对面的车站B需走斑马线DC,已知马路宽CD=20米,超市A到马路边DE的距离AE=10米,车站B到马路边CF的距离BF=40米,且∠BCF=54°,∠ADE=30°.试求从超市A出发,沿A→D→C→B到车站共行走的路程.(结果精确到1米.参考数据:sin54°≈0.80,cos54°≈0.60,tan54°≈1.40)
如图,从超市A到马路对面的车站B需走斑马线DC,已知马路宽CD=20米,超市A到马路边DE的距离AE=10米,车站B到马路边CF的距离BF=40米,且∠BCF=54°,∠ADE=30°.试求从超市A出发,沿A→D→C→B到车站共行走的路程.(结果精确到1米.参考数据:sin54°≈0.80,cos54°≈0.60,tan54°≈1.40)查看答案和解析>>
科目:初中数学 来源: 题型:
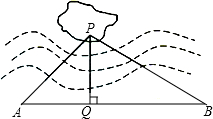 如图,某湖中有一孤立的小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PQ通往小岛,某同学在观光道AB上测得如下数据:AB=100米,∠PAB=45°,∠PBA=30.请求出小桥PQ的长.(
如图,某湖中有一孤立的小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PQ通往小岛,某同学在观光道AB上测得如下数据:AB=100米,∠PAB=45°,∠PBA=30.请求出小桥PQ的长.(| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com