
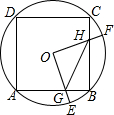
 如图,边长为2的正方形ABCD内接于⊙O,点E是$\widehat{AB}$上一点(不与A、B重合),点F是$\widehat{BC}$上一点,连接OE,OF,分别与AB,BC交于点G,H,有下列结论:
如图,边长为2的正方形ABCD内接于⊙O,点E是$\widehat{AB}$上一点(不与A、B重合),点F是$\widehat{BC}$上一点,连接OE,OF,分别与AB,BC交于点G,H,有下列结论:分析 连接OC、OB、CF、BE.
①先证明$\widehat{BE}$=$\widehat{CF}$,由$\widehat{AB}$=$\widehat{BC}$即可证明结论①正确;
②证明△BOG≌△COH即可解决问题;
③只要证明S四边形OGBH=S△BOC=$\frac{1}{4}$S正方形ABCD=定值即可;
④求出∠BOG的度数,由扇形的面积减去三角形的面积即可得出结论.
解答 解:如图所示,连接OC、OB、CF、BE.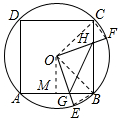
∵∠BOE+∠BOF=90°,∠COF+∠BOF=90°,
∴∠BOE=∠COF,
∴$\widehat{BE}$=$\widehat{CF}$,
∵$\widehat{AB}$=$\widehat{BC}$,
∴$\widehat{AE}$=$\widehat{BF}$;故①正确,
在△BOG与△COH中,
$\left\{\begin{array}{l}{∠BOG=∠COH}\\{OC=OB}\\{∠OBG=∠OCH=45°}\end{array}\right.$,
∴△BOG≌△COH(ASA),
∴OG=OH,∵∠HOG=90°
∴△OGH是等腰直角三角形,②正确,
∴S△OBG=S△OCH,
∴S四边形OGBH=S△BOC=$\frac{1}{4}$S正方形ABCD=定值,故③错误;
作OM⊥AB于M,则OM=BM=$\frac{1}{2}$AB=1,OB=$\sqrt{2}$OM=$\sqrt{2}$,
∴GM=$\frac{\sqrt{3}}{3}$,
∴tan∠GOM=$\frac{GM}{OM}$=$\frac{\sqrt{3}}{3}$,
∴∠GOM=30°,
∵∠BOM=45°,
∴∠BOG=45°-30°=15°,
∴扇形BOE的面积=$\frac{15π×(\sqrt{2})^{2}}{360}$=$\frac{π}{12}$,
∵BG=1-$\frac{\sqrt{3}}{3}$,
∴AG=1+$\frac{\sqrt{3}}{3}$,
过G作GP⊥BO于P,
∴PG=PB=$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{6}}{6}$,
∴△OBG的面积=$\frac{1}{2}$×$\sqrt{2}$×($\frac{\sqrt{2}}{2}$-$\frac{\sqrt{6}}{6}$)=$\frac{1}{2}$-$\frac{\sqrt{3}}{6}$,
∴BG,GE,$\widehat{BE}$围成的面积=扇形BOE的面积-△BOG的面积=$\frac{π}{12}$-$\frac{1}{2}$+$\frac{\sqrt{3}}{6}$,故④错误.
故答案为:①②.
点评 本题考查了正方形的性质、全等三角形的判定和性质、等腰直角三角形的判定和性质、四边形的面积、三角函数、扇形面积公式等知识,本题综合性强,有一定难度,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
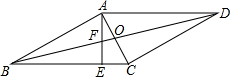 如图,在平行四边形ABCD中,对角线AC、BD交于点O、AC⊥AB、∠ABC=30°,过点A作AE⊥BC于点E,交BD于点F,则$\frac{AF}{AO}$=$\frac{4\sqrt{3}}{7}$.
如图,在平行四边形ABCD中,对角线AC、BD交于点O、AC⊥AB、∠ABC=30°,过点A作AE⊥BC于点E,交BD于点F,则$\frac{AF}{AO}$=$\frac{4\sqrt{3}}{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
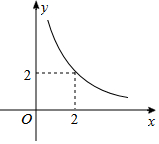 设△ABC的一边长为x,这条边上的高为y,y与x满足的反比例函数关系如图所示.当△ABC为等腰直角三角形时,x+y的值为( )
设△ABC的一边长为x,这条边上的高为y,y与x满足的反比例函数关系如图所示.当△ABC为等腰直角三角形时,x+y的值为( )| A. | 4 | B. | 5 | C. | 5或3$\sqrt{2}$ | D. | 4或3$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
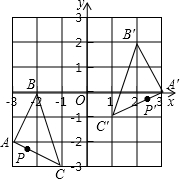 如图,把△ABC经过一定变换得到△A′B′C′,如果△A′B′C′中,B′C′边上一点P′的坐标为(m,n),那么P′点在△ABC中的对应点P的坐标为( )
如图,把△ABC经过一定变换得到△A′B′C′,如果△A′B′C′中,B′C′边上一点P′的坐标为(m,n),那么P′点在△ABC中的对应点P的坐标为( )| A. | (-m,n+2) | B. | (-m,n-2) | C. | (-m-2,-n) | D. | (-m-2,n-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2a+2b=-2(a+b) | B. | a2-2a+4=(a-2)2 | C. | (2a2)3=6a6 | D. | 3a2•2a3=6a5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 含A:10% | 含A(30%) | |
| 成本(元/个) | 1875 | 1775 |
| 出厂价 | 2450 | 2350 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com