
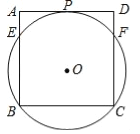
【题目】如图,过正方形ABCD顶点B,C的⊙O与AD相切于点P,与AB,CD分别相交于点E、F,连接EF.
(1)求证:PF平分∠BFD.
(2)若tan∠FBC=![]() ,DF=
,DF=![]() ,求EF的长.
,求EF的长.
【答案】(1)详见解析;(2)![]() .
.
【解析】
试题分析:(1)根据切线的性质得到OP⊥AD,由四边形ABCD的正方形,得到CD⊥AD,推出OP∥CD,根据平行线的性质得到∠PFD=∠OPF,由等腰三角形的性质得到∠OPF=∠OFP,根据角平分线的定义即可得到结论;(2)由∠C=90°,得到BF是⊙O的直径,根据圆周角定理得到∠BEF=90°,推出四边形BCFE是矩形,根据矩形的性质得到EF=BC,根据切割线定理得到PD2=DFCD,于是得到结论.
试题解析:(1)连接OP,BF,PF,
∵⊙O与AD相切于点P,
∴OP⊥AD,
∵四边形ABCD的正方形,
∴CD⊥AD,
∴OP∥CD,
∴∠PFD=∠OPF,
∵OP=OF,
∴∠OPF=∠OFP,
∴∠OFP=∠PFD,
∴PF平分∠BFD;
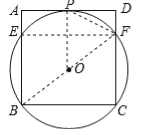
(2)连接EF,
∵∠C=90°,
∴BF是⊙O的直径,
∴∠BEF=90°,
∴四边形BCFE是矩形,
∴EF=BC,
∵AB∥OP∥CD,BO=FO,
∴OP=![]() AD=
AD=![]() CD,
CD,
∵PD2=DFCD,即(![]() )2=
)2=![]() CD,
CD,
∴CD=4![]() ,
,
∴EF=BC=4![]() .
.


科目:初中数学 来源: 题型:
【题目】已知在纸面上有一数轴(如图),折叠纸面.
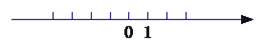
(1)若1表示的点与-1表示的点重合,则-2表示的点与数 表示的点重合;
(2)若-1表示的点与3表示的点重合,回答以下问题:
① 5表示的点与数 表示的点重合;
② 若数轴上A、B两点之间的距离为9(A在B的左侧),且A、B两点经折叠后重合,求A、B两点表示的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年永康市举行的“众泰杯”半程马拉松竞赛约有8000名运动员参赛,把8000用科学记数法表示为( )
A. 0.8×104 B. 8×104 C. 0.8×103 D. 8×103
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个射手连续射靶10次,其中3次射中10环,3次射中9环,4次射中8环.则该射手射中环数的中位数和众数分别为( )
A.8,9B.9,8C.8.5,8D.8.5,9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列实际情景运用了三角形稳定性的是( )
A.人能直立在地面上
B.校门口的自动伸缩栅栏门
C.古建筑中的三角形屋架
D.三轮车能在地面上运动而不会倒
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com