
【题目】已知Rt△ABC,AB=AC,点D在△ABC的外部,且∠DAC<90°,
(1)如图1,若AD=AC,求∠BDC;
(2)如图2,点E在线段AC上,线段DE的垂直平分线交BC的延长线于点P.当点D正好和点B关于线段AC的中点对称时,
①证明:△PDE为直角三角形;
②连接BE、AD,若![]() ,直接写出
,直接写出![]() =_____.
=_____.
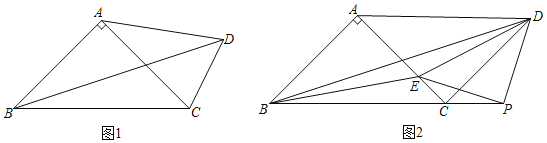
【答案】(1)∠BDC=45°;(2)①证明见解析;②8.
【解析】
(1)设∠DAC=x,则∠BAD=90°+x,由等腰三角形的性质可得∠ADB=45°﹣![]() ,∠ADC=90°﹣
,∠ADC=90°﹣![]() ,即可求解;
,即可求解;
(2)①如图2,过点P作PH⊥CD,PG⊥AC,由中心对称的性质可得AO=CO,BO=DO,可证△AOB≌△COD,可得AB=CD,∠BAC=∠ACD=90°,由“AAS”可证△PHC≌△PGC,可得PH=PG,由“HL”可证Rt△PEG≌Rt△PDH,可得∠EPG=∠HPD,即可得结论;
②设BC=8a,BP=11a,则CP=3a,由等腰直角三角形的性质可求AB=AC=CD=4![]() a,CH=HP=CG=GP=
a,CH=HP=CG=GP=![]() a,可求AE,EC的长,由三角形的面积公式可求解.
a,可求AE,EC的长,由三角形的面积公式可求解.
解:(1)设∠DAC=x,则∠BAD=90°+x,
∵AD=AC=AB,
∴∠ADB=45°﹣![]() ,∠ADC=90°﹣
,∠ADC=90°﹣![]() ,
,
∴∠BDC=∠ADC﹣∠ADB=45°;
(2)如图2,过点P作PH⊥CD,PG⊥AC

∵线段DE的垂直平分线交BC的延长线于点P.
∴EP=DP,
∵点D正好和点B关于线段AC的中点O对称,
∴AO=CO,BO=DO,且∠AOB=∠COD,
∴△AOB≌△COD(SAS)
∴AB=CD,∠BAC=∠ACD=90°,
∵AB=AC,∠BAC=90°,
∴∠ACB=45°,且∠ACD=90°,
∴∠PCG=∠PCH=45°,且PC=PC,∠PGC=∠PHC=90°,
∴△PHC≌△PGC(AAS)
∴PH=PG,且EP=DP,
∴Rt△PEG≌Rt△PDH(HL),
∴∠EPG=∠HPD,
∵∠HCG=∠HCP+∠GCP=90°,PH⊥CD,PG⊥AC,
∴∠HPG=90°,
∴∠EPG+∠EPH=90°,
∴∠DPH+∠EPH=90°,即∠DPE=90°
∴△PDE为直角三角形;
②如图2,

∵![]() ,
,
∴设BC=8a,BP=11a,则CP=3a,
∵AB=AC,∠BAC=90°,BC=8a,
∴AB=AC=4![]() a,
a,
∴CD=4![]() a,
a,
∵∠PCH=∠PCG=45°,PH⊥CD,PG⊥AC,
∴∠PCH=∠PCG=∠HPC=∠GCP=45°,
∴CH=HP,CG=GP,且CP=3a,PH⊥CD,PG⊥AC,
∴CH=HP=CG=GP=![]() a,
a,
∴DH=CD﹣CH=![]() a,
a,
∵Rt△PEG≌Rt△PDH,
∴EG=DH=![]() a,
a,
∴EC=EG﹣CG=![]() a,
a,
∴AE=![]() a,
a,
∴![]() =
=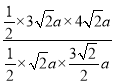 =8,
=8,
故答案为8.


科目:初中数学 来源: 题型:
【题目】已知如图,四边形ABCD为平行四边形,AD=a,AC为对角线,BM∥AC,过点D作 DE∥CM,交AC的延长线于F,交BM的延长线于E.
(1)求证:△ADF≌△BCM;
(2)若AC=2CF,∠ADC=60°,AC⊥DC,求四边形ABED的面积(用含a的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边△ABC的边长为4,以AB为直径的圆交BC于点F,以C为圆心,CF的长为半径作圆,D是⊙C上一动点,E为BD的中点,当AE最大时,BD的长为( )

A. 2![]() B. 2
B. 2![]() C. 2
C. 2![]() +1 D. 6
+1 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)在一个不透明的纸箱里装有红、黄、蓝三种颜色的小球,它们除颜色外完全相同,其中红球有2个,黄球有1个,蓝球有1个.现有一张电影票,小明和小亮决定通过摸球游戏定输赢(赢的一方得电影票).游戏规则是:两人各摸1次球,先由小明从纸箱里随机摸出1个球,记录颜色后放回,将小球摇匀,再由小亮随机摸出1个球并记录颜色.若两人摸到的球颜色相同,则小明赢,否则小亮赢.这个游戏规则对双方公平吗?请你利用树状图或列表法说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
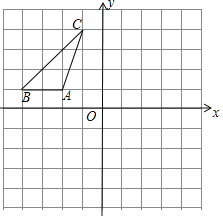
【题目】在平面直角坐标系中,如图所示A(﹣2,1),B(﹣4,1),C(﹣1,4).
(1)△ABC向上平移一个单位,再向左平移一个单位得到△A1B1C1,那么C的对应点C1的坐标为_____;P点到△ABC三个顶点的距离相等,点P的坐标为______;
(2)△ABC关于第一象限角平分线所在的直线作轴对称变换得到△A2B2C2,那么点B的对应点B2的坐标为______;
(3)△A3B3C3是△ABC绕坐标平面内的Q点顺时针旋转得到的,且A3(1,0),B3(1,2),C3(4,﹣1),点Q的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
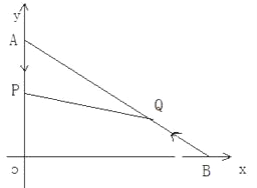
【题目】如图,在平面直角坐标系中,已知点A(0,12),B(16,0),动点P从点A开始在线段AO上以每秒1个单位的速度向点O移动,同时点Q从点B开始在BA上以每秒2个单位的速度向点A移动,设点P、Q移动的时间为t秒.
⑴求直线AB的解析式;
⑵求t为何值时,△APQ与△AOB相似?
⑶当t为何值时,△APQ的面积为![]() 个平方单位?
个平方单位?
⑷当t为何值时,△APQ的面积最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
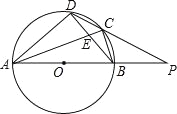
【题目】如图,四边形ABCD内接于⊙O,AB是⊙O的直径,AC和BD相交于点E,且DC2=CECA.
(1)求证:BC=CD;
(2)分别延长AB,DC交于点P,若PB=OB,CD=2![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解方程组的部分过程,回答下列问题
解方程组![]()
现有两位同学的解法如下:
解法一;由①,得x=2y+5,③
把③代入②,得3(2y+5)﹣2y=3.……
解法二:①﹣②,得﹣2x=2.……
(1)解法一使用的具体方法是________,解法二使用的具体方法是______,以上两种方法的共同点是________.
(2)请你任选一种解法,把完整的解题过程写出来
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B是双曲线y=![]() (k>0)上的点,A、B两点的横坐标分别是a、3a,线段AB的延长线交x轴于点C,若S△AOC=3.则k的值为( )
(k>0)上的点,A、B两点的横坐标分别是a、3a,线段AB的延长线交x轴于点C,若S△AOC=3.则k的值为( )
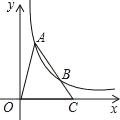
A. 2 B. 1.5 C. 4 D. 6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com